Tehon, virran ja jännitteen laskeminen: elinolojen laskennan periaatteet ja esimerkit

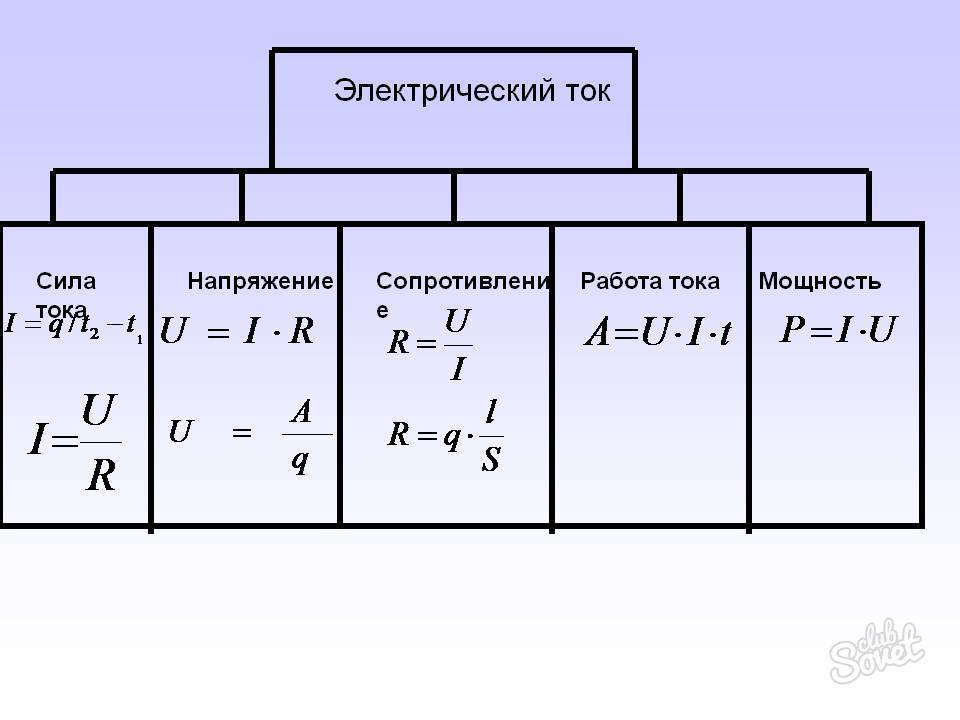
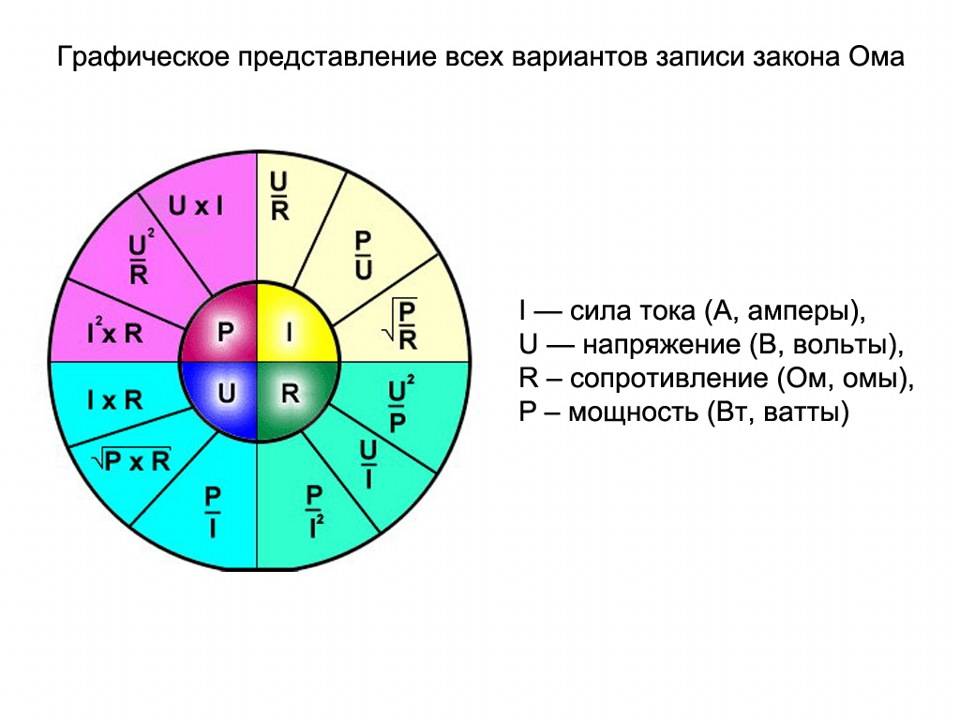
Laskelma rinnakkais- ja sarjakytkennästä

Elektronisen laitteen piiriä laskettaessa on usein tarpeen löytää teho, joka vapautuu yhdestä elementistä. Sitten sinun on määritettävä, mikä jännite putoaa siinä, jos puhumme sarjaliitännästä tai mikä virta kulkee rinnakkain kytkettynä, harkitsemme erityistapauksia.

Tässä Itotal on yhtä suuri kuin:

I=U/(R1+R2)=12/(10+10)=12/20=0,6

Yleinen teho:

P=UI=12*0,6=7,2 wattia

Jokaisella vastuksella R1 ja R2, koska niiden vastus on sama, jännite laskee:

U = IR = 0,6 * 10 = 6 volttia

Ja erottuu seuraavista:

P_{vastuksen päällä}\u003d UI \u003d 6 * 0,6 \u003d 3,6 wattia

Sitten rinnakkaisyhteydellä tällaisessa järjestelmässä:

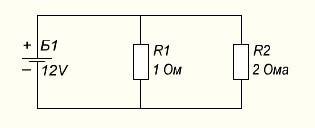
Ensin etsimme I:tä jokaisesta haarasta:

minä₁=U/R₁= 12/1 = 12 ampeeria

minä₂=U/R₂= 12/2 = 6 ampeeria

Ja erottuu jokaisesta seuraavista:

P_R1\u003d 12 * 6 \u003d 72 wattia

P_R2\u003d 12 * 12 \u003d 144 wattia

Kaikki erottuvat:

P=UI=12*(6+12)=216 wattia

Tai kokonaisvastuksen kautta, sitten:

R_yleistä=(R₁*R₂)/( R₁+R₂)=(1*2)/(1+2)=2/3=0,66 ohmia

I = 12/0,66 = 18 ampeeria

P = 12 * 18 = 216 wattia

Kaikki laskelmat täsmäävät, joten löydetyt arvot ovat oikein.

Nykyinen laskelma

Virran suuruus lasketaan teholla ja on tarpeen asunnon - asunnon, talon - suunnitteluvaiheessa.

• Sen syöttökaapelin (johtimen) valinta, jonka kautta virrankulutuslaitteet voidaan liittää verkkoon, riippuu tämän arvon arvosta.
• Kun tiedät sähköverkon jännitteen ja sähkölaitteiden täyden kuorman, on mahdollista laskea kaavan avulla johtimen (johdin, kaapeli) läpi kulkevan virran voimakkuus. Suonten poikkileikkauspinta-ala valitaan sen koon mukaan.

Jos asunnon tai talon sähkönkuluttajat tunnetaan, on suoritettava yksinkertaiset laskelmat, jotta virtapiiri voidaan asentaa oikein.

Samanlaisia ​​laskelmia tehdään tuotantotarkoituksiin: kaapelisydämien vaaditun poikkipinta-alan määrittäminen teollisuuslaitteita (erilaiset teollisuussähkömoottorit ja -mekanismit) kytkettäessä.

ESIMERKKEJÄ tehtävistä

Osa 1

1. Johtimessa olevan virran voimakkuutta lisättiin 2 kertaa. Miten siinä vapautuvan lämmön määrä aikayksikköä kohti muuttuu johtimen resistanssin pysyessä muuttumattomana?

1) kasvaa 4 kertaa
2) vähenee 2 kertaa
3) kasvaa 2 kertaa
4) vähennä 4 kertaa

2.Sähkökiuasspiraalin pituus pieneni 2 kertaa. Miten spiraalissa vapautuvan lämmön määrä aikayksikköä kohti muuttuu vakioverkkojännitteellä?

1) kasvaa 4 kertaa
2) vähenee 2 kertaa
3) kasvaa 2 kertaa
4) vähennä 4 kertaa

3. Vastuksen resistanssi ​\(R_1 \)​ on neljä kertaa pienempi kuin vastuksen vastus ​\(R_2 \)​. Nykyinen työ vastuksessa 2

1) 4 kertaa enemmän kuin vastuksessa 1
2) 16 kertaa enemmän kuin vastus 1
3) 4 kertaa vähemmän kuin vastuksessa 1
4) 16 kertaa vähemmän kuin vastuksessa 1

4. Vastuksen resistanssi ​\(R_1 \)​ on 3 kertaa vastuksen resistanssi ​\(R_2 \)​. Lämmön määrä, joka vapautuu vastuksessa 1

1) 3 kertaa enemmän kuin vastuksessa 2
2) 9 kertaa enemmän kuin vastus 2
3) 3 kertaa vähemmän kuin vastuksessa 2
4) 9 kertaa vähemmän kuin vastuksessa 2

5. Piiri kootaan sarjaan kytketystä virtalähteestä, hehkulampusta ja ohuesta rautalangasta. Lamppu palaa kirkkaammin, jos

1) vaihda lanka ohuemmalla raudalla
2) lyhennä langan pituutta
3) vaihda johto ja hehkulamppu
4) vaihda rautalanka nikromilla

6. Kuvassa on pylväskaavio. Se näyttää jännitearvot kahden saman vastuksen johtimen (1) ja (2) päissä. Vertaa näiden johtimien nykyisen työn \( A_1 \) ja \( A_2 \) arvoja saman ajan.

1) ​\(A_1=A_2 \)​
2) \( A_1 = 3A_2 \)
3) \( 9A_1=A_2 \)
4) \( 3A_1=A_2 \)

7. Kuvassa on pylväskaavio. Se näyttää virranvoimakkuuden arvot kahdessa saman vastuksen johtimessa (1) ja (2). Vertaa näiden johtimien nykyisiä työarvoja \( A_1 \)​ ja \ ( A_2 \) samaan aikaan.

1) ​\(A_1=A_2 \)​
2) \( A_1 = 3A_2 \)
3) \( 9A_1=A_2 \)
4) \( 3A_1=A_2 \)

8. Jos käytät kattokruunussa 60 ja 100 W tehoisia lamppuja huoneen valaisemiseen,

V. Suuri virta on 100 W lampussa.
B. 60 W lamppu vastustaa enemmän.

Tosi(t) on(ovat) väite(t)

1) vain A
2) vain B
3) sekä A että B
4) ei A eikä B

9. Tasavirtalähteeseen kytketty sähköliesi kuluttaa 108 kJ energiaa 120 sekunnissa. Mikä on laattaspiraalin virranvoimakkuus, jos sen vastus on 25 ohmia?

1) 36 A
2) 6 A
3) 2,16 A
4) 1,5 A

10. Sähkökiuas, jonka virta on 5 A, kuluttaa 1000 kJ energiaa. Kuinka kauan virta kulkee laatan spiraalin läpi, jos sen vastus on 20 ohmia?

1) 10 000 s
2) 2000-luku
3) 10 s
4) 2 s

11. Sähkökiukaan niklattu patteri vaihdettiin saman pituiseen ja poikkipinta-alaltaan samankokoiseen nikromikierukkaan. Muodosta vastaavuus fyysisten suureiden ja niiden mahdollisten muutosten välille, kun laatta liitetään sähköverkkoon. Kirjoita taulukkoon valitut numerot vastaavien kirjainten alle. Vastauksen numerot voivat toistua.

FYSIKAALINEN MÄÄRÄ
A) käämin sähkövastus
B) sähkövirran voimakkuus spiraalissa
B) laattojen kuluttama sähkövirta

MUUTOKSEN LUONNE
1) lisääntynyt
2) vähentynyt
3) ei ole muuttunut

12. Muodosta vastaavuus fysikaalisten suureiden ja kaavojen välillä, joilla nämä suuret määritetään. Kirjoita taulukkoon valitut numerot vastaavien kirjainten alle.

FYSIKAALISET MÄÄRÄT
A) työvirta
B) virran voimakkuus
b) nykyinen teho

KAAVA
1) ​\( \frac{q}{t} \)​
2) ​\(qU \)​
3) \( \frac{RS}{L} \)​
4) ​\(UI \)​
5) \( \frac{U}{I} \)​

Osa 2

13.Kiuas on kytketty sarjaan 7,5 ohmin reostaatin kanssa verkkoon, jonka jännite on 220 V. Mikä on lämmittimen vastus, jos reostaatin sähkövirran teho on 480 W?

Kokonaisteho ja sen komponentit

Sähköteho on määrä, joka vastaa sähkön muutos- tai siirtonopeudesta. Näennäinen teho on merkitty kirjaimella S ja se löytyy virran ja jännitteen tehollisten arvojen tulona. Sen mittayksikkö on volttiampeeri (VA; VA).

Näennäisteho voi koostua kahdesta komponentista: aktiivisesta (P) ja loistehosta (Q).

Pätöteho mitataan watteina (W; W), loisteho mitataan varsina (Var).

Se riippuu siitä, minkä tyyppinen kuorma sisältyy virrankulutusketjuun.

Resistiivinen kuorma

Tämän tyyppinen kuorma on elementti, joka vastustaa sähkövirtaa. Tämän seurauksena virta lämmittää kuormaa ja sähkö muunnetaan lämmöksi. Jos minkä tahansa vastuksen vastus on kytketty sarjaan akun kanssa, suljetun piirin läpi kulkeva virta lämmittää sitä, kunnes akku tyhjenee.

Huomio! Vaihtovirtaverkkojen aktiivisena kuormana voidaan antaa esimerkki sähkölämmityksestä (TENA). Lämmön hajoaminen siinä on seurausta sähkön työstä

Tällaisia ​​kuluttajia ovat myös hehkulamppukelat, sähköliesi, uunit, silitysraudat, kattilat.

kapasitiivinen kuorma

Tällaiset kuormat ovat laitteita, jotka voivat kerätä energiaa sähkökenttiin ja luoda voiman liikkeen (värähtelyn) lähteestä kuormaan ja päinvastoin.Kapasitiiviset kuormat ovat kondensaattoreita, kaapelilinjoja (johtimien välinen kapasitanssi), kondensaattoreita ja induktoreja, jotka on kytketty sarjaan ja rinnan piirissä. Audiotehovahvistimet, synkroniset sähkömoottorit yliviritetyssä tilassa kuormittavat myös kapasitiivisen komponentin linjoja.

Induktiivinen kuorma

Kun sähkön kuluttaja on tietty laite, joka sisältää:

• muuntajat;
• kolmivaiheiset asynkroniset moottorit, pumput.

Laitteeseen kiinnitetyissä levyissä näkyy sellainen ominaisuus kuin cos ϕ. Tämä on vaihesiirtokerroin virran ja jännitteen välillä siinä vaihtovirtaverkossa, johon laite liitetään. Sitä kutsutaan myös tehokertoimeksi, mitä lähempänä cos ϕ yksikköä, sitä parempi.

Tärkeä! Kun laite sisältää induktiivisia tai kapasitiivisia komponentteja: muuntajia, kuristimia, käämejä, kondensaattoreita, sinimuotoinen virta jää jännitteestä jonkin verran vaihekulmaa jäljessä. Ihannetapauksessa kapasitanssi tarjoaa -900 vaihesiirron ja induktanssi - + 900

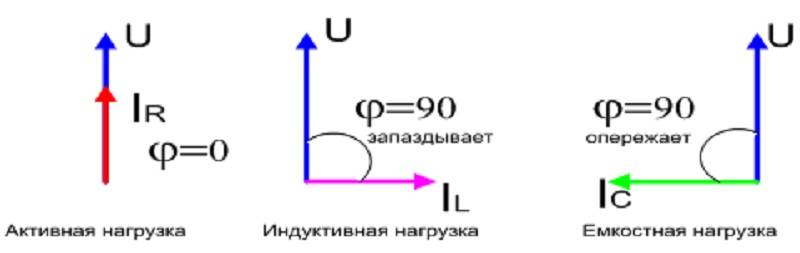Cos ϕ -arvot kuormituksen tyypistä riippuen

Kapasitiiviset ja induktiiviset komponentit muodostavat yhdessä loistehoa. Sitten kokonaistehon kaava on:

S = √ (P2 + Q2),

missä:

• S on näennäisteho (VA);
• P on aktiivinen osa (W);
• Q on reaktiivinen osa (Var).

Jos näytät tämän graafisesti, voit nähdä, että P:n ja Q:n vektorilisäys on S:n täysi arvo - tehokolmion hypotenuusa.

Graafinen selitys täyden tehon olemuksesta

Sähköpiirit ja niiden lajikkeet

Sähköpiiri on joukko laitteita ja yksittäisiä esineitä, jotka on kytketty tietyllä tavalla. Ne tarjoavat polun sähkön kulkua varten.Kunkin yksittäisen johtimen sisällä jonkin aikaa virtaavan varauksen ja tämän ajan keston välisen suhteen karakterisoimiseksi käytetään tiettyä fyysistä määrää. Ja tämä on virta sähköpiirissä.

Tällaisen ketjun kokoonpanoon kuuluu energialähde, energiankuluttajat, ts. kuorma ja johdot. Ne on jaettu kahteen lajikkeeseen:

• Haaroittumaton - generaattorista energiankuluttajalle siirtyvän virran arvo ei muutu. Tämä on esimerkiksi valaistus, joka sisältää vain yhden hehkulampun.
• Haaroittuneet - ketjut, joissa on joitain oksia. Lähteestä liikkuva virta jaetaan ja menee kuormaan useita haaroja pitkin. Sen merkitys kuitenkin muuttuu.

Esimerkki on valaistus, joka sisältää monivartisen kattokruunun.

Haara on yksi tai useampi sarjaan kytketty komponentti. Virran liike siirtyy solmusta, jossa on korkea jännite, solmuun, jolla on vähimmäisarvo. Tässä tapauksessa solmussa tuleva virta on sama kuin lähtevä virta.

Piirit voivat olla epälineaarisia ja lineaarisia. Jos ensimmäisessä on yksi tai useampi elementti, joissa arvot ovat riippuvaisia ​​virrasta ja jännitteestä, niin toisessa elementtien ominaisuuksilla ei ole tällaista riippuvuutta. Lisäksi piireissä, joille on ominaista tasavirta, sen suunta ei muutu, mutta vaihtovirran olosuhteissa se muuttuu ottaen huomioon aikaparametrin.

Ominaisuudet

Vaihtovirta kulkee piirin läpi ja muuttaa sen suuntaa suuruuden mukaan. Luo magneettikentän. Siksi sitä kutsutaan usein jaksolliseksi sinimuotoiseksi vaihtosähkövirraksi. Kaarevan viivan lain mukaan sen arvo muuttuu tietyn ajan kuluttua. Siksi sitä kutsutaan sinimuotoiseksi. On omat asetukset.Tärkeimmistä kannattaa määrittää jakso taajuudella, amplitudilla ja hetkellisellä arvolla.

Jakso on aika, jonka aikana sähkövirrassa tapahtuu muutos, jonka jälkeen se toistuu uudelleen. Taajuus on jakso sekunnissa. Se mitataan hertseinä, kilohertseinä ja millihertseinä.

Amplitudi - virran maksimiarvo jännitteellä ja virtaustehokkuudella koko jakson aikana. Hetkellinen arvo - vaihtovirta tai jännite, joka esiintyy tietyssä ajassa.

AC tekniset tiedot

AC:lle

Vaihtovirtapiirissä on kuitenkin otettava huomioon kokonais-, aktiivinen ja loisarvo sekä tehokerroin (cosF). Käsittelimme kaikkia näitä käsitteitä yksityiskohtaisemmin tässä artikkelissa.

Huomaamme vain, että yksivaiheisen verkon virran ja jännitteen kokonaistehon löytämiseksi sinun on kerrottava ne:

S=UI

Tulos saadaan volttiampeereina, jotta voidaan määrittää aktiivinen teho (watti), sinun on kerrottava S cosФ-kertoimella. Se löytyy laitteen teknisestä dokumentaatiosta.

P=UIcos

Loistehon (loisjännite-ampeerien) määrittämiseen käytetään sinФ cosФ sijaan.

Q=UIsin

Tai ilmaista tästä lausekkeesta:

Ja laske tästä haluamasi arvo.

Tehon löytäminen kolmivaiheisessa verkossa ei myöskään ole vaikeaa; S:n (yhteensä) määrittämiseksi käytä virran ja vaihejännitteen laskentakaavaa:

S = 3U_f/_f

Ja tietäen Ulinearin:

S=1,73*U_lminä_l

1,73 tai 3:n juuri - tätä arvoa käytetään kolmivaiheisten piirien laskemiseen.

Sitten analogisesti löytääksesi P aktiivisena:

P = 3U_f/_f*cosФ=1,73*U_lminä_l*cosФ

Loisteho voidaan määrittää:

Q = 3U_f/_f*sinФ=1,73*U_lminä_l*sinФ

Tämä lopettaa teoreettisen tiedon ja siirrymme käytäntöön.

yksi.Tehonhäviön ja virtausvirran laskin vastuksen ja jännitteen mukaan.

Ohmin lain reaaliaikainen demo.
Viitteeksi
Tässä esimerkissä voit lisätä piirin jännitettä ja vastusta. Nämä reaaliaikaiset muutokset muuttavat piirissä kulkevan virran määrää ja vastukseen haihtunutta tehoa.
Jos tarkastelemme äänijärjestelmiä, sinun on muistettava, että vahvistin tuottaa tietyn jännitteen tietylle kuormitukselle (resistanssille). Näiden kahden suuren suhde määrää tehon.
Vahvistin voi tuottaa rajoitetun määrän jännitettä sisäisestä virtalähteestä ja virtalähteestä riippuen. Teho, jonka vahvistin voi syöttää tietylle kuormitukselle (esimerkiksi 4 ohmia), on myös tarkasti rajoitettu.
Saadaksesi lisää tehoa, voit kytkeä vahvistimeen kuorman, jolla on pienempi vastus (esim. 2 ohmia). Huomaa, että käytettäessä kuormaa, jolla on pienempi vastus - sanotaan kahdesti (se oli 4 ohmia, siitä tuli 2 ohmia) - teho myös kaksinkertaistuu (edellyttäen, että tämä teho voidaan tarjota sisäisestä virtalähteestä ja virtalähteestä).
Jos otamme esimerkiksi 100 watin monovahvistimen 4 ohmin kuormaan tietäen, että se pystyy syöttämään kuormaan enintään 20 voltin jännitteen.
Jos laitat liukusäätimiä laskimeemme
Jännite 20 volttia
Resistanssi 4 ohmia
Sinä tulet saamaan
Teho 100 wattia
 
Jos siirrät vastuksen liukusäädintä 2 ohmia, näet tehon kaksinkertaistuvan 200 wattiin.
Yleisessä esimerkissä virtalähde on akku (ei äänenvahvistin), mutta virran, jännitteen, vastuksen ja vastuksen riippuvuudet ovat samat kaikissa piireissä.
 

Sähköpiirien laskenta

Kaikki sähköpiirien laskemiseen käytetyt kaavat seuraavat toisistaan.

Sähköisten ominaisuuksien suhteet

Joten esimerkiksi teholaskentakaavan mukaan voit laskea virranvoimakkuuden, jos P ja U tunnetaan.

Saadaksesi selville, mitä virtaa 220 V verkkoon kytketty rauta (1100 W) kuluttaa, sinun on ilmaistava virran voimakkuus tehokaavasta:

I = P/U = 1100/220 = 5 A.

Kun tiedät sähkökiuasspiraalin lasketun resistanssin, löydät P-laitteen. Teho resistanssin läpi saadaan kaavasta:

P = U2/R.

On olemassa useita menetelmiä, jotka mahdollistavat tehtävien ratkaisemisen laskemalla tietyn piirin erilaisia ​​parametreja.

Sähköpiirien laskentamenetelmät

Tehon laskenta erityyppisille virtapiireille auttaa arvioimaan oikein voimalinjojen kuntoa. Kotitalous- ja teollisuuslaitteet, jotka on valittu annettujen parametrien Pnom ja S mukaan, toimivat luotettavasti ja kestävät enimmäiskuormituksen vuosia.

Kuinka säästää rahaa

Kahden tariffin mittarin asentaminen säästää sähkön lämmityskustannuksia. Kiinteillä sähkölämmitysasennuksilla varustettujen asuntojen ja talojen Moskovan tariffit erottavat kaksi kustannusta:

1. 4.65 r klo 7.00-23.00.
2. 1.26 r klo 23.00-7.00.

Sitten kulutat kellon ympäri käynnistettyä sähkökattilaa 9 kW kolmannekselle tehosta:

9*0.3*12*4.65 + 9*0.3*12*1.26 = 150 + 40 = 190 ruplaa

Päivittäisen kulutuksen ero on 80 ruplaa. Kuukaudessa säästät 2400 ruplaa. Mikä oikeuttaa kahden tariffin mittarin asennuksen.

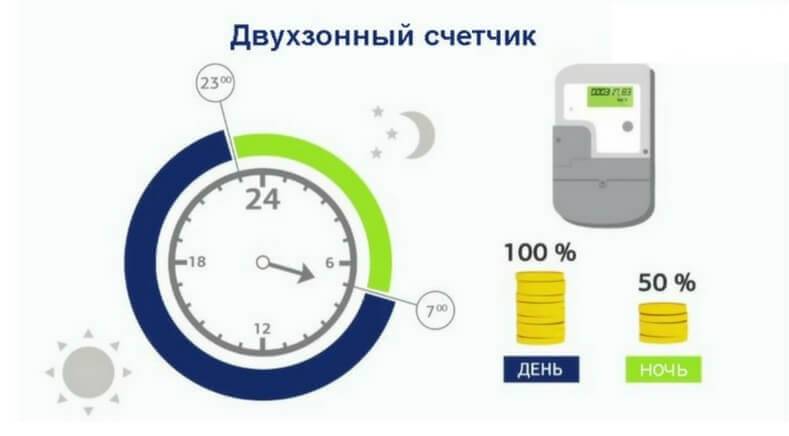
Toinen tapa säästää rahaa käytettäessä kahden tariffin mittaria on käyttää sähkölaitteiden automaattisia ohjauslaitteita. Se koostuu sähkökattilan, kattilan ja muiden asioiden huippukulutuksen osoittamisesta yöllä, jolloin suurin osa sähköstä veloitetaan 1,26, eikä 4,65. Kun olet töissä, kattila voi joko sammua kokonaan tai toimia alhaisen virrankulutuksen tilassa, esimerkiksi 10 % teholla. Sähkökattilan toiminnan automatisoimiseksi voit käyttää ohjelmoitavia digitaalisia termostaatteja tai kattiloita, joilla on mahdollisuus ohjelmoida.

Lopuksi haluaisin huomauttaa, että talon lämmitys sähköllä on melko kallis menetelmä riippumatta tietystä menetelmästä, olipa kyseessä sähkökattila, konvektori tai muu sähkölämmitin. He tulevat hänen luokseen vain tapauksissa, joissa kaasuun ei ole mahdollista muodostaa yhteyttä. Sähkökattilan käyttökustannusten lisäksi sinulla on ensimmäiset kustannukset kolmivaiheisen sähkösyötön rekisteröimisestä.

Päätyöt ovat:

• asiakirjapaketin toteuttaminen, mukaan lukien tekniset tiedot, sähköprojekti jne.;
• maadoituksen järjestäminen;
• talon liittämiseen ja uuden johdotuksen kytkemiseen tarvittavan kaapelin hinta;
• laskurin asennus.

Lisäksi saatat evätä kolmivaihesyötön ja tehonlisäyksen, jos alueellasi ei ole tällaista teknistä mahdollisuutta, kun muuntaja-asemat toimivat jo äärirajoillaan. Kattilan ja lämmityksen tyypin valinta ei riipu vain toiveistasi, vaan myös infrastruktuurin ominaisuuksista.

Tämä päättää lyhyen artikkelimme. Toivomme, että nyt sinulle on tullut selväksi, mikä on sähkökattilan todellinen sähkönkulutus ja kuinka voit alentaa talon lämmityskustannuksia sähköllä.

Lohkojen lukumäärä: 18 | Merkkejä yhteensä: 24761
Käytettyjen luovuttajien määrä: 7
Jokaisen luovuttajan tiedot:

Resistanssin muutos:

Seuraavasta kaaviosta näet resistanssieron kuvan oikealla ja vasemmalla puolella olevien järjestelmien välillä. Venttiili vastustaa hanan vedenpaineen vastusta, venttiilin avautumisasteesta riippuen vastus muuttuu.

Johtimen resistanssi esitetään johtimen kapenemisena, mitä kapeampi johdin, sitä enemmän se vastustaa virran kulkua.

Saatat huomata, että jännite ja vedenpaine ovat samat piirin oikealla ja vasemmalla puolella.

Sinun on kiinnitettävä huomiota tärkeimpään tosiasiaan. Resistanssista riippuen virta kasvaa ja pienenee.

Resistanssista riippuen virta kasvaa ja pienenee.

Vasemmalla, kun venttiili on täysin auki, näemme suurimman vesivirran. Ja pienimmällä resistanssilla näemme suurimman elektronivirran (ampeerin) johtimessa.

Oikealla venttiili on kiinni paljon enemmän ja myös veden virtaus on kasvanut paljon.

Myös johtimen kapeneminen puolittui, mikä tarkoittaa, että virran vastus on kaksinkertaistunut. Kuten näemme, kaksi kertaa vähemmän elektroneja virtaa johtimen läpi suuren vastuksen vuoksi.

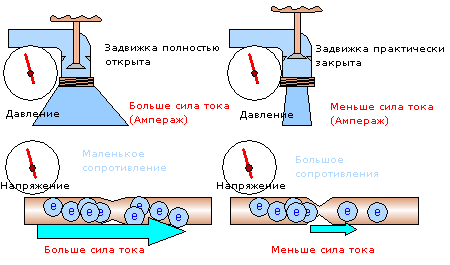
Viitteeksi

Huomaa, että kaaviossa näkyvää johtimen kavennusta käytetään vain esimerkkinä virranvirtauksen resistanssista. Todellisissa olosuhteissa johtimen kapeneminen ei juurikaan vaikuta virtaavaan virtaan

Puolijohteet ja eristeet voivat tarjota paljon suuremman vastuksen.

Kaavion kartiomainen johdin on esitetty vain esimerkkinä meneillään olevan prosessin olemuksen ymmärtämiseksi Ohmin lain kaava on vastuksen ja virran voimakkuuden riippuvuus

I=E/R
Kuten kaavasta näkyy, virran voimakkuus on kääntäen verrannollinen piirin vastukseen.

Enemmän vastusta = vähemmän virtaa
 

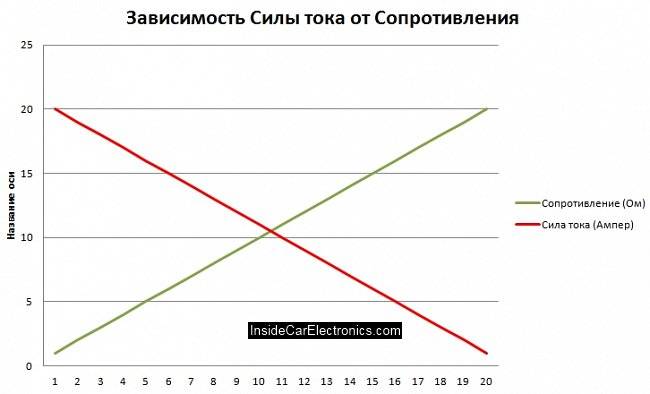
* edellyttäen, että jännite on vakio.
 

Kaavojen käyttäminen

Tämä kulma luonnehtii vaihesiirtoa muuttuvissa U-piireissä, jotka sisältävät induktiivisia ja kapasitiivisia elementtejä. Aktiivisten ja reaktiivisten komponenttien laskemiseen käytetään trigonometrisiä funktioita, joita käytetään kaavoissa. Ennen kuin tulos lasketaan näillä kaavoilla, on tarpeen laskea tai Bradis-taulukoita käyttäen määrittää sin φ ja cos φ. Sen jälkeen kaavojen mukaan

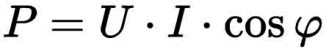
Lasken sähköpiirin halutun parametrin. Mutta on otettava huomioon, että jokainen näiden kaavojen mukaan laskettu parametri, joka johtuu U:sta, joka muuttuu jatkuvasti harmonisten värähtelyjen lakien mukaan, voi ottaa joko hetkellisen, neliön keskiarvon tai väliarvon. . Yllä esitetyt kolme kaavaa ovat voimassa virran ja U:n rms-arvoille. Kumpikin kahdesta muusta arvosta on tulos laskentamenettelystä, jossa käytetään erilaista kaavaa, joka ottaa huomioon ajan t kulumisen:

Mutta tässä ei ole kaikki vivahteet. Esimerkiksi voimalinjoille käytetään kaavoja, jotka sisältävät aaltoprosesseja. Ja ne näyttävät erilaisilta. Mutta se on täysin eri tarina...

AC:lle

Vaihtovirtapiirissä on kuitenkin otettava huomioon kokonais-, aktiivinen ja loisarvo sekä tehokerroin (cosF). Käsittelimme kaikkia näitä käsitteitä yksityiskohtaisemmin tässä artikkelissa.

Huomaamme vain, että yksivaiheisen verkon virran ja jännitteen kokonaistehon löytämiseksi sinun on kerrottava ne:

S=UI

Tulos saadaan volttiampeereina, jotta voidaan määrittää aktiivinen teho (watti), sinun on kerrottava S cosФ-kertoimella.Se löytyy laitteen teknisestä dokumentaatiosta.

P=UIcos

Loistehon (loisjännite-ampeerien) määrittämiseen käytetään sinФ cosФ sijaan.

Q=UIsin

Tai ilmaista tästä lausekkeesta:

Ja laske tästä haluamasi arvo.

Tehon löytäminen kolmivaiheisessa verkossa ei myöskään ole vaikeaa; S:n (yhteensä) määrittämiseksi käytä virran ja vaihejännitteen laskentakaavaa:

Ja tietäen Ulinearin:

1,73 tai 3:n juuri - tätä arvoa käytetään kolmivaiheisten piirien laskemiseen.

Sitten analogisesti löytääksesi P aktiivisena:

Loisteho voidaan määrittää:

Tämä lopettaa teoreettisen tiedon ja siirrymme käytäntöön.

Kysymyksiä työstä ja sähköstä

Teoreettiset kysymykset sähkövirran toiminnalle ja teholle voivat olla seuraavat:

1. Mikä on sähkövirran työn fysikaalinen määrä? (Vastaus annetaan yllä olevassa artikkelissamme).
2. Mikä on sähkövoima? (Vastaus yllä).
3. Määrittele Joule-Lenzin laki. Vastaus: Kiinteän johtimen, jonka resistanssi on R, läpi kulkevan sähkövirran työ muuttuu johtimessa lämmöksi.
4. Miten virran toimintaa mitataan? (Vastaus yllä).
5. Miten teho mitataan? (Vastaus yllä).

Tämä on esimerkkiluettelo kysymyksistä. Fysiikan teoreettisten kysymysten ydin on aina sama: tarkistaa fysikaalisten prosessien ymmärtäminen, suuren riippuvuus toisesta, kansainvälisessä SI-järjestelmässä omaksuttujen kaavojen ja mittayksiköiden tuntemus.

Mielenkiintoista tietoa aiheesta

Tuotannossa käytetään kolmivaiheista virtalähdejärjestelmää. Tällaisen verkon kokonaisjännite on 380 V. Myös tällaiset johdotukset asennetaan monikerroksisiin rakennuksiin ja jaetaan sitten asuntojen kesken. Mutta on yksi vivahde, joka vaikuttaa verkon lopulliseen jännitteeseen - sydämen liittäminen jännitteen alaisena johtaa 220 V:iin.Kolmivaiheinen, toisin kuin yksivaiheinen, ei aiheuta vääristymiä teholaitteita kytkettäessä, koska kuorma jakautuu suojassa. Mutta kolmivaiheisen verkon tuomiseksi omakotitaloon tarvitaan erityinen lupa, joten kahden ytimen järjestelmä on laajalle levinnyt, joista yksi on nolla.

AC Power Norms

Jännite ja teho ovat mitä jokaisen kerros- tai omakotitalossa asuvan tulee tietää. Asunnon ja omakotitalon vakiovaihtojännite ilmaistaan ​​220 ja 380 wattia. Mitä tulee sähköenergian voimakkuuden kvantitatiivisen mittauksen määrittämiseen, jännitteeseen on lisättävä sähkövirta tai mitattava vaadittu indikaattori wattimittarilla. Samanaikaisesti, jotta voit tehdä mittauksia viimeisellä laitteella, sinun on käytettävä antureita ja erikoisohjelmia.

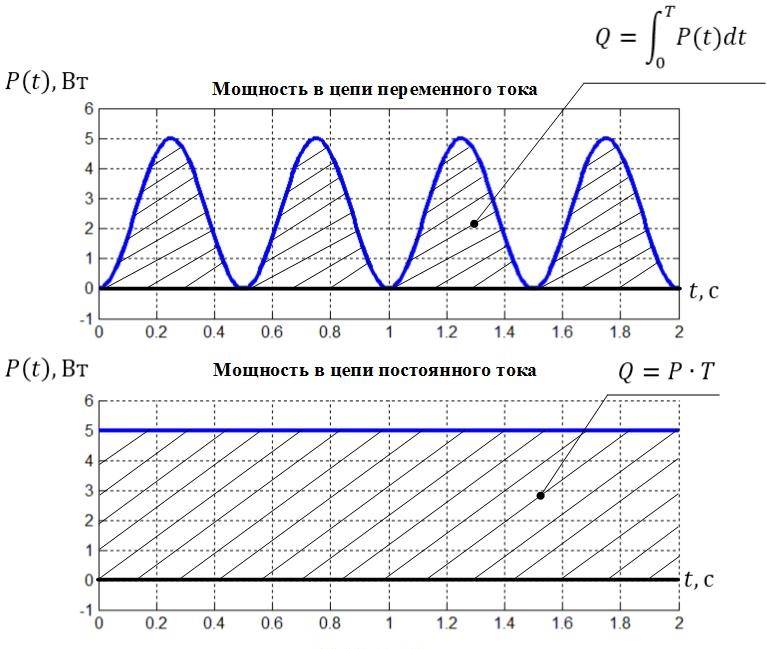Mikä on AC Power

Vaihtovirta määräytyy virran määrän suhteella ajassa, joka tuottaa työtä tietyssä ajassa. Tavallinen käyttäjä käyttää sähköenergian toimittajan hänelle välittämää tehoilmaisinta. Yleensä se on 5-12 kilowattia. Nämä luvut riittävät varmistamaan tarvittavien kotitalouksien sähkölaitteiden toimivuuden.

Tämä indikaattori riippuu siitä, mitkä ulkoiset olosuhteet talon energian toimittamiselle, mitkä virtarajoituslaitteet (automaattiset tai puoliautomaattiset laitteet) on asennettu, jotka säätelevät hetkeä, jolloin tehosäiliöt saapuvat kuluttajalähteeseen. Tämä tehdään eri tasoilla kodin sähköpaneelista keskussähkönjakeluyksikköön.

Tehonormit vaihtovirtaverkossa

Sähköpiirin muunnosmenetelmä

Kuinka määrittää virranvoimakkuus monimutkaisten piirien yksittäisissä piireissä? Käytännön ongelmien ratkaisemiseksi ei aina ole tarpeen selventää kunkin elementin sähköisiä parametreja. Laskelmien yksinkertaistamiseksi käytetään erityisiä muunnostekniikoita.

Piirin laskenta yhdellä teholähteellä

Sarjakytkennässä käytetään esimerkissä tarkasteltujen sähköisten vastusten summaa:

Req = R1 + R2 + ... + Rn.

Silmukkavirta on sama missä tahansa piirin kohdassa. Voit tarkistaa sen ohjausosan katkosta yleismittarilla. Kuitenkin jokaisessa yksittäisessä elementissä (eri arvoilla) laite näyttää erilaista jännitettä. Tekijä: Kirchhoffin toinen laki voit tarkentaa laskentatulosta:

E = Ur1 + Ur2 + Urn.

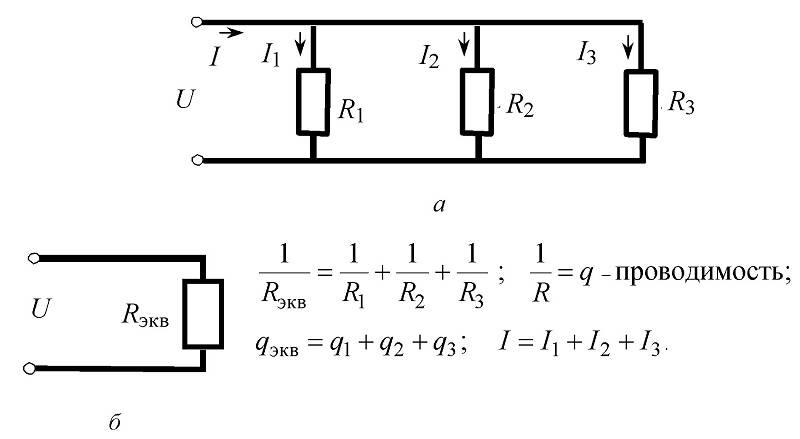Rinnakkaiskytkentä vastusten, piirien ja laskukaavat

Tässä muunnelmassa täysin Kirchhoffin ensimmäisen postulaatin mukaisesti virrat erotetaan ja yhdistetään tulo- ja lähtösolmuissa. Kaaviossa näkyvä suunta on valittu ottaen huomioon kytketyn akun napaisuus. Edellä käsiteltyjen periaatteiden mukaisesti piirin yksittäisten komponenttien jännitetasaisuuden perusmääritelmä säilyy.

Seuraava esimerkki osoittaa, kuinka löytää virta yksittäisistä haaroista. Laskemiseen otettiin seuraavat alkuarvot:

• R1 = 10 ohmia;
• R2 = 20 ohm;
• R3 = 15 ohm;
• U = 12 V.

Seuraava algoritmi määrittää piirin ominaisuudet:

peruskaava kolmelle elementille:

Rtot = R1*R2*R3/(R1*R2 + R2*R3 + R1*R3.

• korvaamalla tiedot, laske Rtot = 10 * 20 * 15 / (10 * 20 + 20 * 15 + 10 * 15) = 3000 / (200 + 300 + 150) = 4,615 ohmia;
• I \u003d 12 / 4,615 ≈ 2,6 A;
• I1 \u003d 12 / 10 \u003d 1,2 A;
• I2 = 12/20 = 0,6 A;
• I3 = 12/15 = 0,8 A.

Kuten edellisessä esimerkissä, on suositeltavaa tarkistaa laskentatulos.Komponentteja kytkettäessä rinnan on huomioitava tulovirtojen ja kokonaisarvon yhtäläisyys:

I \u003d 1,2 + 0,6 + 0,8 \u003d 2,6 A.

Jos käytetään sinimuotoista lähdesignaalia, laskelmat monimutkaistuvat. Kun muuntaja liitetään yksivaiheiseen 220 V pistorasiaan, on otettava huomioon häviöt (vuoto) lepotilassa. Tässä tapauksessa käämien induktiiviset ominaisuudet ja kytkentä- (muunnos)kerroin ovat olennaisia. Sähkövastus (XL) riippuu seuraavista parametreista:

• signaalin taajuus (f);
• induktanssi (L).

Laske XL kaavalla:

XL \u003d 2π * f * L.

Kapasitiivisen kuorman vastuksen löytämiseksi lauseke sopii:

Xc \u003d 1 / 2π * f * C.

Ei pidä unohtaa, että piireissä, joissa on reaktiivisia komponentteja, virran ja jännitteen vaiheet siirtyvät.

Laajan sähköpiirin laskenta useilla virtalähteillä

Tarkastettujen periaatteiden avulla lasketaan monimutkaisten piirien ominaisuudet. Seuraavassa näytetään, kuinka virta löytyy piiristä, kun lähdettä on kaksi:

• nimetä komponentit ja perusparametrit kaikissa piireissä;
• tee yhtälöt yksittäisille solmuille: a) I1-I2-I3=0, b) I2-I4+I5=0, c) I4-I5+I6=0;
• Kirchhoffin toisen postulaatin mukaisesti voidaan kirjoittaa seuraavat lausekkeet ääriviivalle: I) E1=R1 (R01+R1)+I3*R3, II) 0=I2*R2+I4*R4+I6*R7+I3*R3 , III) -E2 = -15*(R02+R5+R6)-14*R4;
• tarkista: d) I3+I6-I1=0, ulkosilmukka E1-E2=I1*(r01+R1)+I2*R2-I5*(R02+R5+R6)+I6*R7.

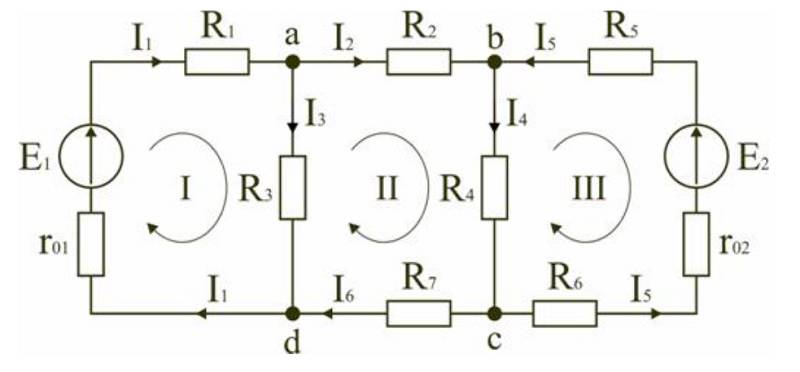Selittävä kaavio laskelmista kahdella lähteellä

Virran laskenta yksivaiheiselle verkolle

Virta mitataan ampeereina. Tehon ja jännitteen laskemiseen käytetään kaavaa I = P/U, jossa P on teho tai kokonaissähkökuorma watteina mitattuna.Tämä parametri on syötettävä laitteen tekniseen passiin. U - edustaa lasketun verkon jännitettä voltteina mitattuna.

Virran ja jännitteen välinen suhde näkyy selvästi taulukossa:

Sähkölaitteet ja -laitteet	Virrankulutus (kW)	Nykyinen (A)
Pesukoneet	2,0 – 2,5	9,0 – 11,4
Kiinteät sähköliesi	4,5 – 8,5	20,5 – 38,6
mikroaaltouunit	0,9 – 1,3	4,1 – 5,9
Astianpesukoneet	2,0 – 2,5	9,0 – 11,4
Jääkaapit, pakastimet	0,14 – 0,3	0,6 – 1,4
Sähköinen lattialämmitys	0,8 – 1,4	3,6 – 6,4
Sähköinen lihamylly	1,1 – 1,2	5,0 – 5,5
Vedenkeitin	1,8 – 2,0	8,4 – 9,0

Siten tehon ja virran voimakkuuden välinen suhde mahdollistaa alustavien kuormituslaskelmien suorittamisen yksivaiheisessa verkossa. Laskentataulukko auttaa sinua valitsemaan tarvittavan lankaosan parametreista riippuen.

Johtimen sydämen halkaisijat (mm)	Johtimen poikkileikkaus (mm2)	Kuparijohtimet	Alumiiniset johtimet
Nykyinen (A)	Teho, kWt)	Vahvuus (A)	Teho, kWt)
0,8	0,5	6	1,3
0,98	0,75	10	2,2
1,13	1,0	14	3,1
1,38	1,5	15	3,3	10	2,2
1,6	2,0	19	4,2	14	3,1
1,78	2,5	21	4.6	16	3,5
2,26	4,0	27	5,9	21	4,6
2,76	6,0	34	7,5	26	5,7
3,57	10,0	50	11,0	38	8,4
4,51	16,0	80	17,6	55	12,1
5,64	25,0	100	22,0	65	14,3

Johtopäätös

Kuten näette, piirin tai sen osan tehon löytäminen ei ole ollenkaan vaikeaa, puhutaanpa sitten vakiosta vai muutoksesta. On tärkeämpää määrittää oikein kokonaisvastus, virta ja jännite

Muuten, tämä tieto riittää jo määrittämään oikein piirin parametrit ja valitsemaan elementit - kuinka monta wattia valitaan vastukset, kaapelien ja muuntajien poikkileikkaukset. Ole myös varovainen laskeessasi S-summaa, kun lasket radikaalilauseketta. Kannattaa vain lisätä, että kun maksamme sähkölaskuja, maksamme kilowattitunteista tai kWh:sta, ne vastaavat tietyn ajanjakson kulutettua tehoa. Jos esimerkiksi liitit 2 kilowatin lämmittimen puoleksi tunniksi, mittari käämittää 1 kW / h ja tunnin ajan - 2 kW / h ja niin edelleen analogisesti.

Lopuksi suosittelemme katsomaan hyödyllisen videon artikkelin aiheesta:

Lue myös:

• Kuinka määrittää laitteiden virrankulutus
• Kuinka laskea kaapeliosuudet
• Tehon ja vastuksen merkintävastukset

Oppitunnin yhteenveto

Tällä oppitunnilla pohdimme erilaisia ​​tehtäviä johtimien sekaresistanssiin sekä sähköpiirien laskemiseen.