- Suljetulle piirille
- Erillinen osa ja täydellinen sähköpiiri
- Sähköpiirin virtaosuuden laskenta
- Laskentavaihtoehto koko ketjulle
- Lain vaikutus muuttujaan
- EMF-lähde täydellisessä piirissä
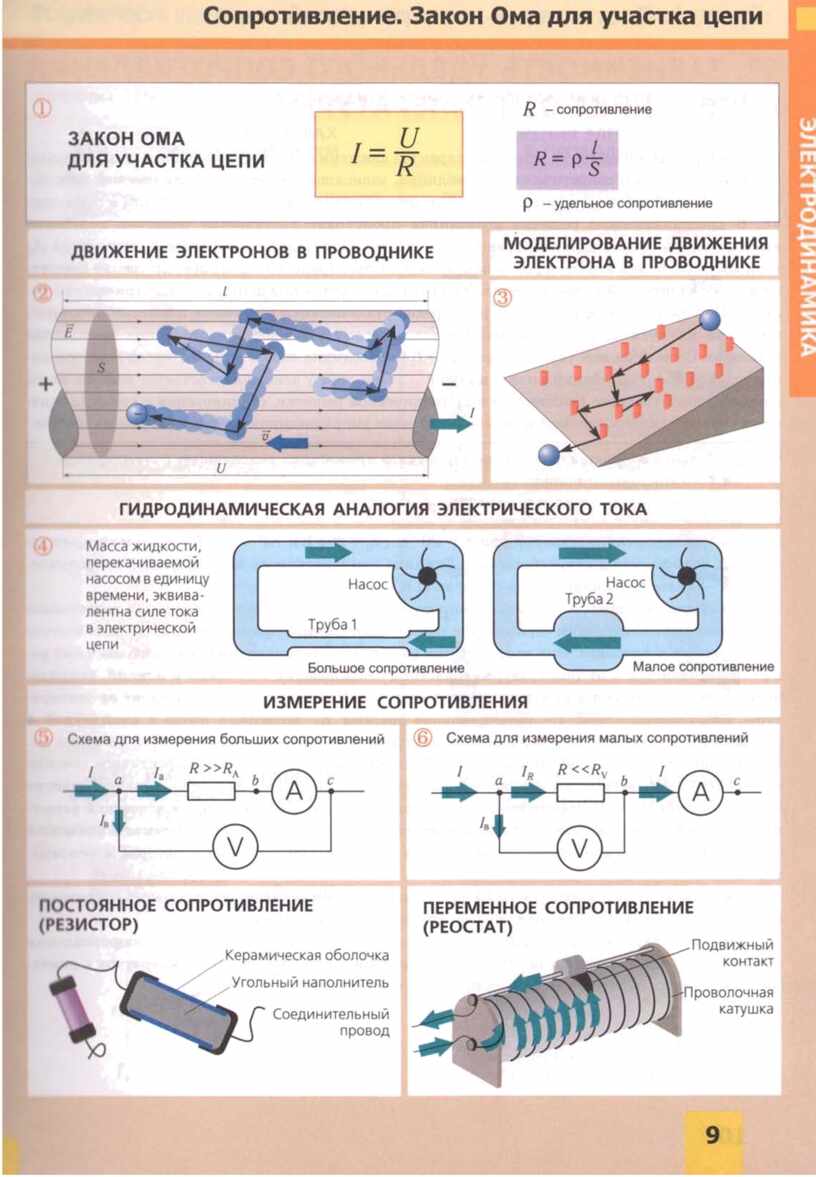
- R - sähkövastus
- DC-piirin epätasainen osa
- Elementtien sarja- ja rinnakkaiskytkentä
- Sarjaan kytkettyjen resistiivisten elementtien ketju
- Rinnakkaisten resistiivisten elementtien ketju
- Lain integraaliset ja differentiaaliset muodot
- Virran ja vastuksen ymmärtäminen
- Ohmin laki vaihtovirralle
- Kun Ohmin laki toteutuu
- Kirchhoffin lait.
- Peruskonseptit
- Voimaa ja jännitystä
- Johtimen vastus
- Ohmin lain tulkinta
- Rinnakkais- ja sarjaliitäntä
- sarjaliitäntä
- Rinnakkaisliitäntä
- Mikä antaa meille rinnakkais- ja sarjayhteyden?
- Ihanteellinen EMF-lähde
- Differentiaalimuodossa
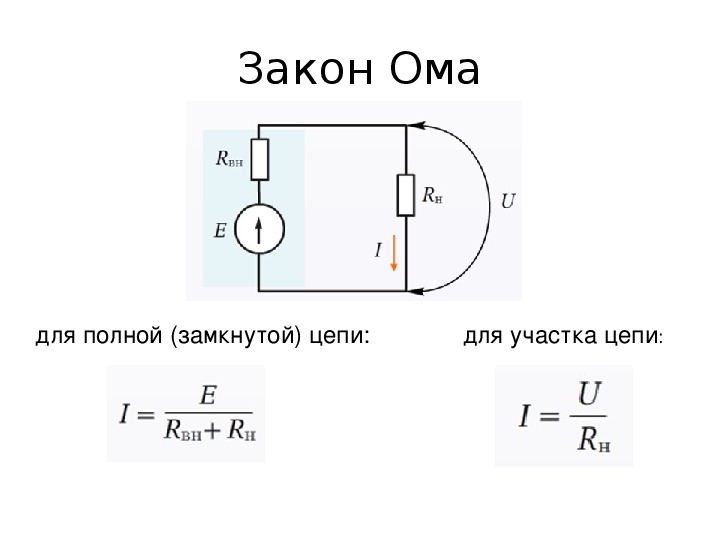
Suljetulle piirille
Suljetulla piirillä tarkoitetaan suljettua sähköliitäntää, jonka kautta virta kiertää. Kun sarja johtoja yhdistää toisiinsa ja täydentää piirin siten, että minä juoksen ympyrän päästä toiseen, se on suljettu piiri.
EMF (E) - ilmaistaan ja mitataan voltteina ja viittaa akun tai magneettisen voiman tuottamaan jännitteeseen Faradayn lain mukaan, jonka mukaan ajassa muuttuva magneettikenttä indusoi sähkövirran.
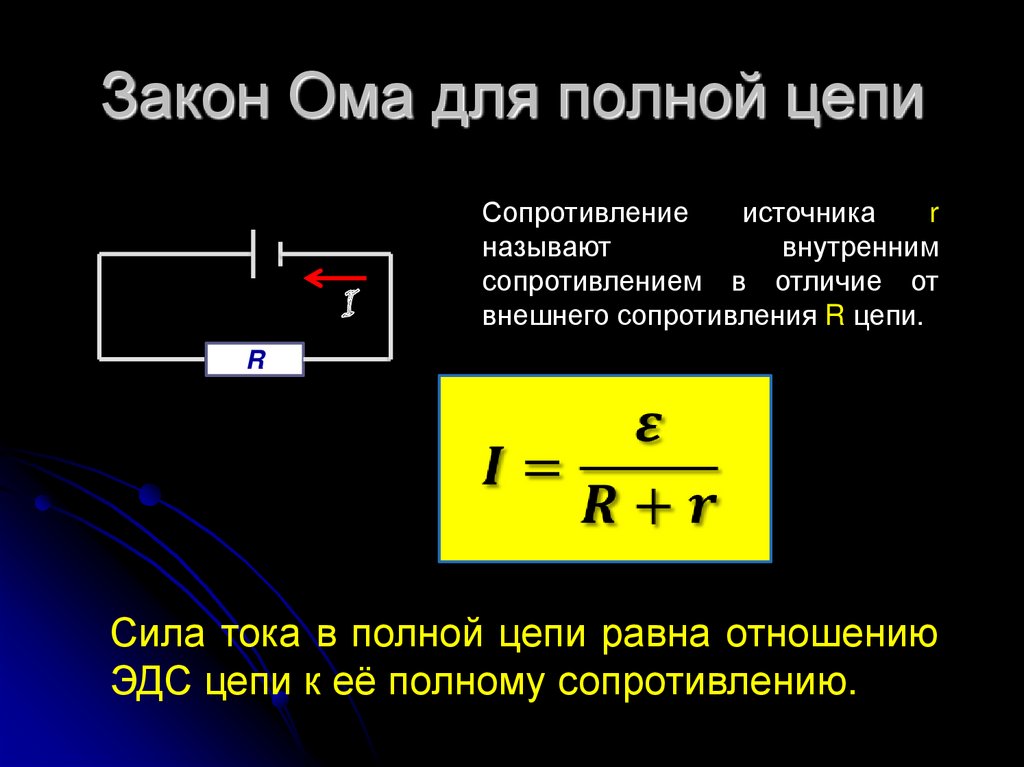
Sitten: E = IR + Ir
E \u003d I (R + r)
I \u003d E / (R + r)
Missä: r on virtalähteen vastus.
Tämä lauseke tunnetaan suljetun silmukan piirien Ohmin laina.
Heterogeeninen ketju
Erillinen osa ja täydellinen sähköpiiri
Ohmin lakia, jota sovelletaan osaan tai koko piiriin, voidaan tarkastella kahdessa laskentavaihtoehdossa:
- Erillinen lyhyt osa. Se on osa piiriä ilman EMF-lähdettä.
- Täydellinen ketju, joka koostuu yhdestä tai useammasta osasta. Tämä sisältää myös EMF-lähteen, jolla on oma sisäinen vastus.
Sähköpiirin virtaosuuden laskenta
Tässä tapauksessa sovelletaan peruskaavaa I \u003d U / R, jossa I on virran voimakkuus, U on jännite, R on vastus. Sen mukaan voidaan muotoilla Ohmin lain yleisesti hyväksytty tulkinta:
Tämä formulaatio on perusta monille muille kaavoille, jotka esitetään niin kutsutulla "kamomillalla" graafisessa suunnittelussa. Sektorissa P - teho määritetään, sektoreissa I, U ja R - suoritetaan virran voimakkuuteen, jännitteeseen ja vastukseen liittyviä toimia.
Jokainen lauseke - sekä perus- että ylimääräinen - antaa sinun laskea piirissä käytettäviksi tarkoitettujen elementtien tarkat parametrit.
Sähköpiirien parissa työskentelevät asiantuntijat määrittävät nopeasti minkä tahansa parametrin kuvassa näkyvällä kolmiomenetelmällä.
Laskelmissa tulee ottaa huomioon osan elementtejä yhdistävien johtimien resistanssi. Koska ne on valmistettu eri materiaaleista, tämä parametri on erilainen kussakin tapauksessa.Jos on tarpeen muodostaa täydellinen piiri, pääkaavaa täydennetään jännitelähteen, esimerkiksi akun, parametreilla.
Laskentavaihtoehto koko ketjulle
Täydellinen piiri koostuu yksittäisistä osista, jotka on yhdistetty yhdeksi kokonaisuudeksi yhdessä jännitelähteen (EMF) kanssa. Siten osien olemassa olevaa vastusta täydentää kytketyn lähteen sisäinen vastus. Siksi aiemmin käsitelty päätulkinta kuuluu seuraavasti: I = U / (R + r). Täällä EMF-lähteen resistiivinen ilmaisin (r) on jo lisätty.
Puhtaan fysiikan näkökulmasta tätä indikaattoria pidetään erittäin pienenä arvona. Käytännössä monimutkaisia piirejä ja piirejä laskettaessa asiantuntijat ovat kuitenkin pakotettuja ottamaan sen huomioon, koska lisävastus vaikuttaa työn tarkkuuteen. Lisäksi kunkin lähteen rakenne on hyvin heterogeeninen, minkä seurauksena resistanssi voidaan joissakin tapauksissa ilmaista melko korkeilla luvuilla.
Yllä olevat laskelmat on tehty DC-piireille. Toimenpiteet ja laskelmat vaihtovirralla tehdään eri kaavion mukaan.
Lain vaikutus muuttujaan
Vaihtovirralla piirin resistanssi on ns. impedanssi, joka koostuu aktiivisesta resistanssista ja reaktiivisesta resistiivisestä kuormasta. Tämä johtuu elementtien läsnäolosta, joilla on induktiiviset ominaisuudet ja sinimuotoinen virta-arvo. Jännite on myös muuttuja, joka toimii kytkentälakiensa mukaan.
Siksi Ohmin lain mukainen AC-piiri lasketaan ottaen huomioon erityiset vaikutukset: virran suuruuden johtaminen tai viivästyminen jännitteestä sekä aktiivisen ja loistehon läsnäolo.Reaktanssi puolestaan sisältää induktiiviset tai kapasitiiviset komponentit.
Kaikki nämä ilmiöt vastaavat kaavaa Z \u003d U / I tai Z \u003d R + J * (XL - XC), jossa Z on impedanssi; R - aktiivinen kuorma; XL, XC - induktiiviset ja kapasitiiviset kuormat; J on korjauskerroin.
EMF-lähde täydellisessä piirissä
Sähkövirran esiintymiseksi suljetussa piirissä tässä piirissä on oltava vähintään yksi erityinen elementti, jossa tapahtuu varausten siirto sen napojen välillä. Voimat, jotka kuljettavat varauksia tämän elementin sisällä, tekevät sen sähkökenttää vastaan, mikä tarkoittaa, että niiden luonteen on oltava erilainen kuin sähköinen. Siksi tällaisia voimia kutsutaan kolmansiksi osapuoliksi.
Riisi. 1. Ulkoiset voimat fysiikassa.
Sähköpiirin elementtiä, jossa ulkoiset voimat toimivat siirtääkseen varauksia sähkökentän vaikutusta vastaan, kutsutaan virtalähteeksi. Sen pääominaisuus on ulkoisten voimien suuruus. Sen karakterisoimiseksi otetaan käyttöön erityinen mitta - sähkömoottorivoima (EMF), se on merkitty kirjaimella $\mathscr{E}$.
Virtalähteen EMF:n arvo on yhtä suuri kuin varauksen siirtoon liittyvien ulkoisten voimien suhde tämän varauksen arvoon:
$$\mathscr{E}={A_{st}\yli q}$$
Koska EMF:n merkitys on hyvin lähellä sähköjännitteen merkitystä (muista, jännite on varausta kuljettavan sähkökentän tekemän työn suhde tämän varauksen arvoon), niin EMF, kuten jännite, mitataan Voltit:
$$1B={J\overCl}$$
Toiseksi tärkein todellisen virtalähteen sähköinen ominaisuus on sen sisäinen vastus.Kun varauksia siirretään napojen välillä, ne ovat vuorovaikutuksessa EMF-lähteen aineen kanssa, ja siksi sähkövirran lähteessä on myös jonkin verran vastusta. Sisäinen vastus, kuten tavallinen vastus, mitataan ohmeina, mutta sitä merkitään pienellä latinalaisella kirjaimella $r$.

Riisi. 2. Esimerkkejä nykyisistä lähteistä.
R - sähkövastus
Resistanssi on jännitteen käänteisluku, ja sitä voidaan verrata vaikutukseen, jolla keho liikutetaan liikettä vastaan juoksevassa vedessä. R:n yksikkö on Om, jota merkitään isolla kreikkalaisella kirjaimella Omega.
Resistanssin käänteisluku (1/R) tunnetaan johtavuutena, joka mittaa esineen kykyä suorittaa varausta Siemens-yksiköissä ilmaistuna.
Käytettyä geometrisesti riippumatonta suuretta kutsutaan resistanssiksi ja sitä merkitään yleensä kreikkalaisella symbolilla r.
Lisäinformaatio. Ohmin laki auttaa määrittämään kolme tärkeää sähköverkon toiminnan indikaattoria, mikä yksinkertaistaa tehon laskemista. Sitä ei voida soveltaa yksipuolisiin verkkoihin, joissa on elementtejä, kuten diodi, transistori ja vastaavat. Eikä se myöskään sovellu epälineaarisille elementeille, joista tyristorit ovat esimerkkejä, koska näiden elementtien resistanssiarvo muuttuu eri jännitteillä ja virroilla.
Korkeammilla taajuuksilla hajautettu käyttäytyminen tulee hallitsevaksi. Sama tapahtuu hyvin pitkien sähkölinjojen kanssa. Jopa niin alhaisella taajuudella kuin 60 Hz, erittäin pitkä siirtojohto, kuten 30 km, on hajautunut. Pääsyynä on se, että piireissä leviävät tehokkaat sähkösignaalit ovat sähkömagneettisia aaltoja, eivät voltteja ja ampeeria, jotka saastuttavat sähkömagneettinen aalto.Johtimet toimivat yksinkertaisesti aaltojen ohjaimina. Joten esimerkiksi koaksiaalikaapeli näyttää Z = 75 ohmia, vaikka sen tasavirtavastus on mitätön.
Ohmin laki on sähkötekniikan peruslaki. Sillä on lukuisia käytännön sovelluksia kaikissa sähköpiireissä ja elektronisissa komponenteissa.
Yleisimmät esimerkit Ohmin lain soveltamisesta:
- Sähkölämmittimeen syötetty teho. Lämmittimen käämin resistanssin ja käytetyn jännitteen perusteella voidaan laskea lämmittimeen syötetty teho.
- Sulakkeiden valinta. Ne ovat suojakomponentteja, jotka on kytketty sarjaan elektronisten laitteiden kanssa. Sulakkeet/CB:t on mitoitettu ampeereina. Nykyinen sulakkeen arvo lasketaan Ohmin lain mukaan.
- Elektronisten laitteiden suunnittelu. Elektroniset laitteet, kuten kannettavat tietokoneet ja matkapuhelimet, vaativat tasavirtalähteen, jolla on tietty virta. Tyypilliset matkapuhelimen akut vaativat 0,7-1 A. Näiden komponenttien läpi kulkevan virran nopeutta ohjataan vastuksen avulla. Ohmin lakia käytetään laskemaan nimellisvirta tyypillisessä piirissä.
Ohmin johtopäätöksistä tuli aikoinaan katalysaattori uudelle sähköalan tutkimukselle, eivätkä ne ole nykyään menettäneet merkitystään, sillä nykyaikainen sähkötekniikka perustuu niihin. Vuonna 1841 Om sai Royal Societyn korkeimman kunnianosoituksen, Copley-mitalin, ja termi "Om" tunnustettiin vastarinnan yksiköksi jo vuonna 1872.
DC-piirin epätasainen osa
Heterogeenisellä rakenteella on sellainen piirin osa, jossa johtimien ja elementtien lisäksi on virtalähde. Sen EMF on otettava huomioon laskettaessa virran kokonaisvoimakkuutta tällä alueella.
On olemassa kaava, joka määrittelee heterogeenisen paikan pääparametrit ja prosessit: q = q0 x n x V. Sen indikaattorit on kuvattu seuraavasti:
- Siirrettäessä varauksia (q) ne saavuttavat tietyn tiheyden. Sen suorituskyky riippuu virran voimakkuudesta ja johtimen poikkileikkausalasta (S).
- Tietyn pitoisuuden (n) olosuhteissa on mahdollista ilmoittaa tarkasti yksittäisen ajanjakson aikana siirrettyjen yksikkölatausten lukumäärä (q0).
- Laskelmissa johdinta pidetään ehdollisesti lieriömäisenä poikkileikkauksena, jolla on jokin tilavuus (V).
Kun liität johdin akkuun, jälkimmäinen purkautuu hetken kuluttua. Eli elektronien liike hidastuu vähitellen ja lopulta pysähtyy kokonaan. Tätä helpottaa johtimen molekyylihila, joka estää elektronien törmäyksen keskenään ja muiden tekijöiden kanssa. Tällaisen vastustuksen voittamiseksi on lisäksi käytettävä tiettyjä kolmannen osapuolen voimia.
Laskelmien aikana nämä voimat lisätään Coulombin voimiin. Lisäksi yksikkövarauksen q siirtämiseksi 1. pisteestä 2:een on suoritettava työ A1-2 tai yksinkertaisesti A12. Tätä tarkoitusta varten luodaan potentiaaliero (ϕ1 - ϕ2). Tasavirtalähteen vaikutuksesta syntyy EMF, joka siirtää varauksia piiriä pitkin. Kokonaisjännityksen suuruus koostuu kaikista edellä mainituista voimista.
Tasavirtalähteen kytkennän napaisuus on otettava huomioon laskelmissa. Kun liittimiä vaihdetaan, myös EMF muuttuu, mikä nopeuttaa tai hidastaa varausten liikettä.
Elementtien sarja- ja rinnakkaiskytkentä
Sähköpiirin elementeille (piirin osalle) ominaismomentti on sarja- tai rinnakkaiskytkentä.
Vastaavasti jokaiseen liitäntätyyppiin liittyy erilainen virta- ja jännitesyöttö. Tässä mielessä Ohmin lakia sovelletaan myös eri tavoin elementtien sisällyttämisvaihtoehdon mukaan.
Sarjaan kytkettyjen resistiivisten elementtien ketju
Sarjakytkennässä (kahdesta komponentista koostuvan piirin osa) käytetään sanamuotoa:
- minä = minä1 = minä2 ;
- U = U1 + U2 ;
- R = R1 + R2
Tämä muotoilu osoittaa selvästi, että riippumatta sarjaan kytkettyjen resistiivisten komponenttien lukumäärästä, piirin osassa kulkeva virta ei muuta arvoa.
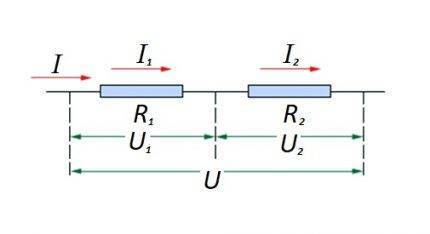 Piiriosan resistiivisten elementtien kytkeminen sarjaan keskenään. Tällä vaihtoehdolla on oma laskentalakinsa. Kaaviossa: I, I1, I2 - virta; R1, R2 - resistiiviset elementit; U, U1, U2 - syötetty jännite
Piiriosan resistiivisten elementtien kytkeminen sarjaan keskenään. Tällä vaihtoehdolla on oma laskentalakinsa. Kaaviossa: I, I1, I2 - virta; R1, R2 - resistiiviset elementit; U, U1, U2 - syötetty jännite
Piirin aktiivisiin resistiivisiin komponentteihin syötetyn jännitteen määrä on summa ja se laskee yhteen EMF-lähteen arvon.
Tässä tapauksessa kunkin yksittäisen komponentin jännite on: Ux = I * Rx.
Kokonaisvastusta tulisi pitää piirin kaikkien resistiivisten komponenttien arvojen summana.
Rinnakkaisten resistiivisten elementtien ketju
Siinä tapauksessa, että resistiiviset komponentit on kytketty rinnakkain, muotoilua pidetään oikeudenmukaisena saksalaisen fyysikon Ohmin lain suhteen:
- minä = minä1 + minä2 … ;
- U = U1 = U2 … ;
- 1/R = 1/R1 + 1/R2 + …
"Mixed"-tyyppisten piiriosien kokoamisvaihtoehtoja ei suljeta pois, kun käytetään rinnakkais- ja sarjaliitäntöjä.
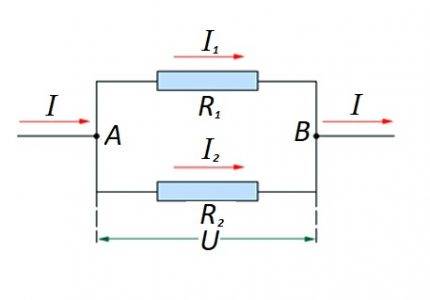 Resistiivisten elementtien kytkeminen piiriosaan rinnakkain. Tähän vaihtoehtoon sovelletaan sen omaa laskentalakia. Kaaviossa: I, I1, I2 - virta; R1, R2 - resistiiviset elementit; U - syötetty jännite; A, B - tulo-/poistumispisteet
Resistiivisten elementtien kytkeminen piiriosaan rinnakkain. Tähän vaihtoehtoon sovelletaan sen omaa laskentalakia. Kaaviossa: I, I1, I2 - virta; R1, R2 - resistiiviset elementit; U - syötetty jännite; A, B - tulo-/poistumispisteet
Tällaisille vaihtoehdoille laskenta suoritetaan yleensä rinnakkaisliitännän resistiivisyyden alustavalla laskennalla. Sitten tulokseen lisätään sarjaan kytketyn vastuksen arvo.
Lain integraaliset ja differentiaaliset muodot
Kaikki yllä olevat kohdat laskelmilla ovat sovellettavissa olosuhteisiin, joissa niin sanotusti "homogeenisen" rakenteen johtimia käytetään osana sähköpiirejä.
Samaan aikaan käytännössä joutuu usein tekemisiin kaavion rakentamisen kanssa, jossa johtimien rakenne muuttuu eri alueilla. Esimerkiksi käytetään suuremman poikkileikkauksen omaavia lankoja tai päinvastoin pienempiä, jotka on valmistettu eri materiaaleista.
Tällaisten erojen huomioon ottamiseksi on olemassa muunnelma niin sanotusta "differentiaali-integraali Ohmin laista". Äärettömän pienelle johtimelle virrantiheystaso lasketaan intensiteetin ja johtavuusarvon mukaan.
Differentiaalilaskelman alla otetaan kaava: J = ό * E
Integraalilaskua varten formulaatio: I * R = φ1 - φ2 + έ
Nämä esimerkit ovat kuitenkin pikemminkin lähempänä korkeamman matematiikan koulukuntaa, eikä niitä varsinaisesti käytetä yksinkertaisen sähköasentajan todellisessa käytännössä.
Virran ja vastuksen ymmärtäminen
Aloitetaan sähkövirran käsitteestä. Lyhyesti sanottuna sähkövirta suhteessa metalleihin on elektronien - negatiivisesti varautuneiden hiukkasten - suunnattua liikettä. Ne esitetään yleensä pieninä ympyröinä.Rauhallisessa tilassa he liikkuvat satunnaisesti ja muuttavat jatkuvasti suuntaaan. Tietyissä olosuhteissa - potentiaalieron ilmaantuessa - nämä hiukkaset aloittavat tietyn liikkeen johonkin suuntaan. Tämä liike on sähkövirtaa.
Selvyyden vuoksi voimme verrata elektroneja johonkin tasoon vuotaneeseen veteen. Niin kauan kuin kone on paikallaan, vesi ei liiku. Mutta heti kun rinne ilmestyi (potentiaaliero syntyi), vesi alkoi liikkua. Sama on elektronien kanssa.
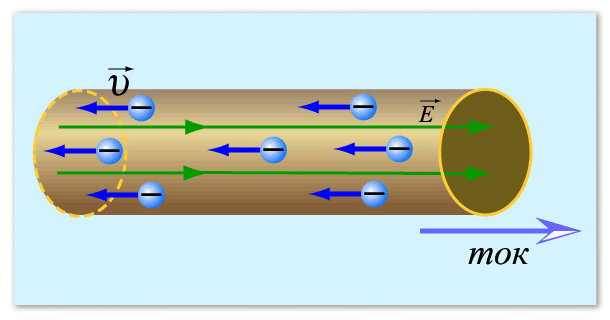
Näin sähkövirta voidaan kuvitella
Nyt meidän on ymmärrettävä, mikä vastus on ja miksi heillä on palautetta virranvoimakkuudesta: mitä suurempi vastus, sitä pienempi virta. Kuten tiedät, elektronit liikkuvat johtimen läpi. Yleensä nämä ovat metallilankoja, koska metallilla on hyvä kyky johtaa sähköä. Tiedämme, että metallilla on tiheä kidehila: monia hiukkasia, jotka ovat lähellä ja liittyvät toisiinsa. Metalliatomien välillä kulkevat elektronit törmäävät niihin, mikä vaikeuttaa niiden liikkumista. Tämä auttaa havainnollistamaan johtimen kohdistamaa vastusta. Nyt käy selväksi, miksi mitä suurempi vastus, sitä pienempi virran voimakkuus - mitä enemmän hiukkasia, sitä vaikeampaa elektronien on voittaa polku, he tekevät sen hitaammin. Tämä näyttää olevan selvitetty.
Jos haluat testata tätä riippuvuutta empiirisesti, etsi muuttuva vastus, kytke sarjaan vastus - ampeerimittari - virtalähde (akku). On myös toivottavaa laittaa piiriin kytkin - tavallinen vaihtokytkin.
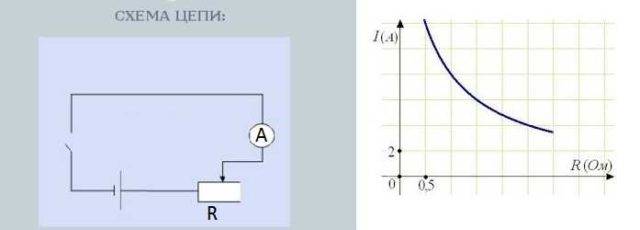
Piiri virran riippuvuuden testaamiseen resistanssista
Vastuksen nupin kääntäminen muuttaa vastusta.Samalla myös virranvoimakkuutta mittaavan ampeerimittarin lukemat muuttuvat. Lisäksi mitä suurempi vastus, sitä vähemmän nuoli poikkeaa - sitä vähemmän virtaa. Mitä pienempi vastus, sitä enemmän nuoli poikkeaa - virta on suurempi.
Virran riippuvuus resistanssista on lähes lineaarinen, eli se heijastuu kaavioon melkein suorana viivana. Miksi melkein - tästä pitäisi keskustella erikseen, mutta se on toinen tarina.
Ohmin laki vaihtovirralle
Vaihtovirtapiirejä laskettaessa resistanssin käsitteen sijaan otetaan käyttöön "impedanssin" käsite. Impedanssi on merkitty kirjaimella Z, se sisältää kuorman R aktiivisen vastuksena ja reaktanssi X (tai Rr). Tämä johtuu sinimuotoisen virran (ja minkä tahansa muun muodon virtojen) muodosta ja induktiivisten elementtien parametreista sekä kytkentälaeista:
- Induktiivisen piirin virta ei voi muuttua välittömästi.
- Kapasitanssin omaavan piirin jännite ei voi muuttua hetkessä.
Näin ollen virta alkaa viivästyä tai johtaa jännitettä, ja näennäinen teho jaetaan aktiiviseen ja loistehon.
U = I/Z
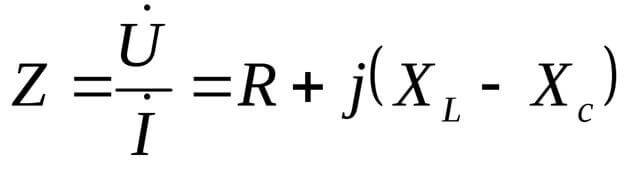
XL ja XC ovat kuorman reaktiivisia komponentteja.
Tässä yhteydessä otetaan käyttöön arvo cosФ:
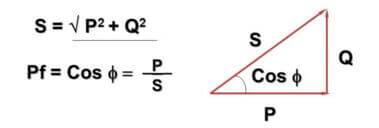
Tässä - Q - loisteho vaihtovirrasta ja induktiivis-kapasitiivisista komponenteista, P - aktiivinen teho (häviöi aktiivisissa komponenteissa), S - näennäisteho, cosФ - tehokerroin.
Olet ehkä huomannut, että kaava ja sen esitys leikkaavat Pythagoraan lauseen. Tämä on totta ja kulma Ф riippuu siitä, kuinka suuri kuorman reaktiivinen komponentti on - mitä suurempi se on, sitä suurempi se on. Käytännössä tämä johtaa siihen, että verkossa todellisuudessa kulkeva virta on suurempi kuin kotitalousmittarin huomioima, kun taas yritykset maksavat täydestä tehosta.
Tässä tapauksessa vastus esitetään monimutkaisessa muodossa:
Tässä j on imaginaarinen yksikkö, joka on tyypillinen yhtälöiden kompleksiselle muodolle. Harvemmin kutsutaan nimellä i, mutta sähkötekniikassa vaihtovirran tehollinen arvo on myös merkitty, joten sekaantumisen välttämiseksi on parempi käyttää j.
Kuvitteellinen yksikkö on √-1. On loogista, että neliöitäessä ei ole sellaista lukua, joka voi johtaa negatiiviseen tulokseen "-1".
Kun Ohmin laki toteutuu
Ihanteellisten olosuhteiden luominen ei ole helppoa. Jopa puhtaissa johtimissa sähkövastus vaihtelee lämpötilan mukaan. Sen väheneminen minimoi kidehilan molekyylien aktiivisuutta, mikä yksinkertaistaa vapaiden varausten liikkumista. Tietyllä "jäätymisen" tasolla esiintyy suprajohtavuuden vaikutus. Päinvastainen vaikutus (johtavuuden heikkeneminen) havaitaan kuumennettaessa.
Samaan aikaan elektrolyytit, metallit ja tietyt keramiikkatyypit säilyttävät sähkövastuksen virrantiheydestä riippumatta. Parametrien stabiilius säilyttäen tietyn lämpötilajärjestelmän mahdollistaa Ohmin lain kaavojen soveltamisen ilman lisäkorjauksia.
Puolijohdemateriaaleille ja kaasuille on ominaista vaihteleva sähkövastus. Tähän parametriin vaikuttaa merkittävästi ohjausvoimakkuuden virran voimakkuus. Suorituskykyominaisuuksien laskemiseen on käytettävä erityisiä laskentamenetelmiä.
Jos vaihtovirta otetaan huomioon, laskentatapa korjataan. Tässä tapauksessa reaktiivisten komponenttien läsnäolo on otettava huomioon. Resistanssin resistanssin vuoksi on mahdollista soveltaa ohmin lain kaavoihin perustuvia tarkasteltuja laskentatekniikoita.
Kirchhoffin lait.
Jakelu
virrat sähköpiirin haaroissa
noudattaa Kirchhoffin ensimmäistä lakia,
ja jännitysten jakautuminen osille
ketju noudattaa Kirchhoffin toista lakia.
Kirchhoffin lait
Ohmin lain ohella tärkeimmät
sähköpiirien teoriassa.
Ensimmäinen
Kirchhoffin laki:
Algebrallinen
solmun virtojen summa on nolla:
i
= 0 (19)
Missä
i
on tietyssä solmussa konvergoivien haarojen lukumäärä.
Eli summaus
ulottuu oksissa oleviin virtoihin,
jotka suppenevat tarkastelussa
solmu.
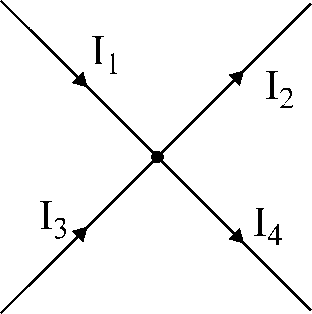
Kuva 17. Kuva
Kirchhoffin ensimmäiseen lakiin.
Määrä
yhtälöt on koottu ensimmäisen mukaan
Kirchhoffin laki määritellään kaavalla:
Nup
= Nu
– 1,
Missä
Nu
on solmujen lukumäärä tarkasteltavassa ketjussa.
Merkkejä virroista sisään
yhtälöt otetaan huomioon valitut
positiivinen suunta. Kyltit klo
Virrat ovat samat, jos virrat ovat samat
suuntautunut tähän
solmu.
Esimerkiksi,
kuvassa 17 esitetylle solmulle:
annamme merkkejä solmuun virtaaville virroille
"+" ja solmusta virtaaviin virtoihin - merkkejä
«-».
Sitten yhtälö
Kirchhoffin ensimmäisen lain mukaan se kirjoitetaan
Niin:
minä1
– Minä2
+ minä3
– Minä4
= 0.
yhtälöt,
koottu Kirchhoffin ensimmäisen lain mukaan,
kutsutaan solmuiksi.
Tämä
laki ilmaisee sen tosiasian, että solmussa
sähkövaraus ei kerry
eikä sitä kuluteta. Sähkön määrä
sivustolle tulevat maksut ovat samat kuin summa
lataukset jättävät solmun yhdessä ja samassa
sama aikaväli.
Toinen
Kirchhoffin laki:
Algebrallinen
summa emf missä tahansa suljetussa piirissä
ketju on yhtä suuri kuin pudotusten algebrallinen summa
jännite tämän piirin elementeissä:
Ui
=
Ei
IiRi=Ei(20)
Missä
i
- elementin numero (resistanssi tai
jännitelähde) tarkastelussa
ääriviivat.
**Määrä
toisen mukaan kootut yhtälöt
Kirchhoffin laki määritellään kaavalla:
Nup
= Huom
- Ei
+ 1 – Ned.s.
Missä
Huom
- sähköpiirin haarojen lukumäärä;
Nu
— solmujen lukumäärä;
Ned.s.
on ihanteellisten emf-lähteiden lukumäärä.
Kuva 18. Kuva
Kirchhoffin toiseen lakiin.
varten,
kirjoittaa toisen lain oikein
Kirchhoff tietylle ääriviivalle seuraa
noudattaa seuraavia sääntöjä:
-
mielivaltaisesti
valitse ääriviivan ohituksen suunta,
esimerkiksi myötäpäivään (kuva 18). -
emf
ja vastaavat jännitehäviöt
valitun suunnan suuntaan
ohitus on kirjoitettu lausekkeessa kanssa
merkki "+"; jos e.f.s. ja jännitehäviö
eivät vastaa suuntaa
ääriviivat, niin niitä edeltää merkki
«-».
Esimerkiksi,
kuvan 18 ääriviivalle, Kirchhoffin toinen laki
kirjoitetaan seuraavasti:
U1
– U2
+ U3
=E1
–E3
–E4
(21)
Yhtälö (20) voi olla
kirjoittaa uudelleen muotoon:
(Ui
-ei)
= 0 (22)
Missä
(U
– E)
- jännitys oksassa.
Näin ollen
Kirchhoffin toinen laki voidaan muotoilla
seuraavalla tavalla:
Algebrallinen
minkä tahansa haarojen jännitteiden summa
suljettu silmukka on nolla.
potentiaalia
aiemmin käsitelty kaavio palvelee
toisen graafinen tulkinta
Kirchhoffin laki.
Tehtävä numero 1.
AT
kuvan 1 piirille on annettu virrat I1
ja minä3,
vastus ja emf Määritä virrat
minä4,
minä5,
minä6
; pisteiden välinen jännite a
ja b
jos minä1
= 10mA,
minä3
= -20 mA,
R4
= 5 kOhm,
E5
= 20 B,
R5
= 3 kOhm,
E6
= 40 B,
R6
= 2kOhm.
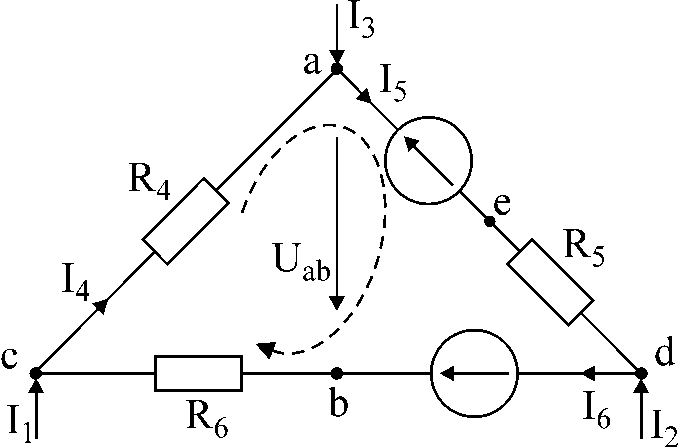
Kuva 1
Ratkaisu:
-
Tietylle
ääriviiva, muodostamme kaksi yhtälöä mukaan
Kirchhoffin ensimmäinen laki ja yksi - mukaan
toinen. Ääriviivan suunta
merkitty nuolella.

AT
ratkaisun tuloksena saamme: I6
= 0; minä4
= 10 mA;
minä5
= -10mA
-
kysyä
jännitteen suunta pisteiden välillä
a
ja b
pisteestä "a"
kohtaan "b"
– Uab.
Tämä jännite löytyy yhtälöstä
Kirchhoffin toinen laki:
minä4R4
+ Uab
+ minä6R6
= 0
Uab
= -50V.
Tehtävä numero 2.
varten
kuvion 2 kaaviot laativat yhtälöitä
Kirchhoffin lait ja määrittelevät tuntemattomat
pisteitä.
Annettu:
minä1
= 20 mA;
minä2
= 10mA
R1
= 5 kOhm,
R3
= 4 kOhm,
R4
= 6 kOhm,
R5
= 2kOhm,
R6
= 4kΩ.
Kuva 2
Ratkaisu:
Solmujen lukumäärä
yhtälöt - 3, ääriviivayhtälöiden lukumäärä
– 1.
Muistaa!
Kun laaditaan yhtälö toisen mukaan
Kirchhoffin laki, valitsemme ääriviivan, sisään
joka ei sisällä nykyisiä lähteitä.
Ääriviivan suunta näkyy kuvassa.
AT
tämän piirin haarojen I virrat1
ja minä2.
Tuntematon
virrat
minä3,
minä4,
minä5,
minä6.

Päättää
järjestelmä, saamme: I3
= 13,75 mA;
minä4
= -3,75 mA;
minä5
= 6,25 mA;
minä6
= 16,25 mA.
Peruskonseptit
Sähkövirta kulkee, kun suljettu piiri sallii elektronien siirtyä korkeasta potentiaalista alempaan piirissä. Toisin sanoen virta vaatii elektronien lähteen, jolla on energiaa saada ne liikkeelle, sekä negatiivisten varausten paluupisteen, jolle on ominaista niiden puute. Fysikaalisena ilmiönä piirissä olevalle virralle on tunnusomaista kolme perussuuretta:
- Jännite;
- nykyinen vahvuus;
- johtimen vastus, jonka läpi elektronit liikkuvat.
Voimaa ja jännitystä
Virran voimakkuus (I, mitattuna ampeereina) on elektronien (varauksen) tilavuus, joka liikkuu tietyn piirin paikan läpi aikayksikköä kohti. Toisin sanoen mittaus I on liikkeessä olevien elektronien lukumäärän määritys
On tärkeää ymmärtää, että termillä tarkoitetaan vain liikettä: esimerkiksi kytkemättömän akun napojen staattisilla varauksilla ei ole mitattavissa olevaa arvoa I. Yhteen suuntaan kulkevaa virtaa kutsutaan suoraksi (DC), ja jaksottaisesti muuttuvaa suuntaa kutsutaan vaihtosuuntaiseksi (AC). Jännitettä voidaan kuvata sellaisella ilmiöllä kuin paine tai painovoiman vaikutuksen alaisena olevien esineiden potentiaalienergian ero
Tämän epätasapainon luomiseksi sinun on ensin käytettävä energiaa, joka toteutuu liikkeessä sopivissa olosuhteissa. Esimerkiksi kuorman putoamisen korkeudesta nostamiseen tehdään töitä, galvaanisissa akuissa potentiaaliero napoihin muodostuu kemiallisen energian muuntamisen seurauksena, generaattoreissa - altistumisen seurauksena sähkömagneettinen kenttä
Stressiä voidaan havainnollistaa sellaisella ilmiöllä kuin paine tai painovoiman vaikutuksen alaisena olevien esineiden potentiaalienergian ero. Tämän epätasapainon luomiseksi sinun on ensin käytettävä energiaa, joka toteutuu liikkeessä sopivissa olosuhteissa. Esimerkiksi kuorman putoamisessa korkealta sen nostotyö toteutuu, galvaanisissa akuissa potentiaaliero napoihin muodostuu kemiallisen energian muuntumisen seurauksena, generaattoreissa - altistumisen seurauksena elektromagneettinen kenttä.
Johtimen vastus
Riippumatta siitä, kuinka hyvä tavallinen johdin on, se ei koskaan päästä elektroneja kulkemaan läpi ilman vastustusta niiden liikkeelle. Vastusta voidaan pitää mekaanisen kitkan analogina, vaikka tämä vertailu ei ole täydellinen.Kun virta kulkee johtimen läpi, jokin potentiaaliero muuttuu lämmöksi, joten vastuksen yli tulee aina jännitehäviö. Sähkölämmittimet, hiustenkuivaajat ja muut vastaavat laitteet on suunniteltu ainoastaan haihduttamaan sähköenergiaa lämmön muodossa.
Yksinkertaistettu vastus (merkitty nimellä R) on mitta siitä, kuinka paljon elektronien virtaus hidastuu piirissä. Se mitataan ohmeina. Vastuksen tai muun elementin johtavuus määräytyy kahdella ominaisuudella:
- geometria;
- materiaalia.
Muoto on äärimmäisen tärkeä, kuten hydraulisesta analogiasta käy ilmi: veden työntäminen pitkän ja kapean putken läpi on paljon vaikeampaa kuin veden työntäminen lyhyen ja leveän putken läpi. Materiaalilla on ratkaiseva rooli. Esimerkiksi elektronit voivat liikkua vapaasti kuparilangassa, mutta ne eivät voi virrata lainkaan eristeiden, kuten kumin, läpi niiden muodosta riippumatta. Geometrian ja materiaalin lisäksi on muitakin tekijöitä, jotka vaikuttavat johtavuuteen.
Ohmin lain tulkinta
Varausten liikkeen varmistamiseksi sinun on suljettava piiri. Jos lisätehoa ei ole, virta ei voi olla olemassa pitkään. Potentiaalit tasoittuvat nopeasti. Piirin toimintatilan ylläpitämiseksi tarvitaan lisälähde (generaattori, akku).
Koko piiri sisältää kaikkien komponenttien kokonaissähkövastuksen. Tarkkoja laskelmia varten otetaan huomioon häviöt johtimissa, resistiivisissä elementeissä ja virtalähteessä.
Kuinka paljon jännitettä on käytettävä tietylle virranvoimakkuudelle, lasketaan kaavalla:
U=I*R.
Vastaavasti tarkasteltujen suhteiden avulla määritetään muut piirin parametrit.
Rinnakkais- ja sarjaliitäntä
Sähkötekniikassa elementit kytketään joko sarjaan - peräkkäin tai rinnan - tämä tarkoittaa, että yhteen pisteeseen on kytketty useita tuloja ja samojen elementtien lähdöt toiseen.
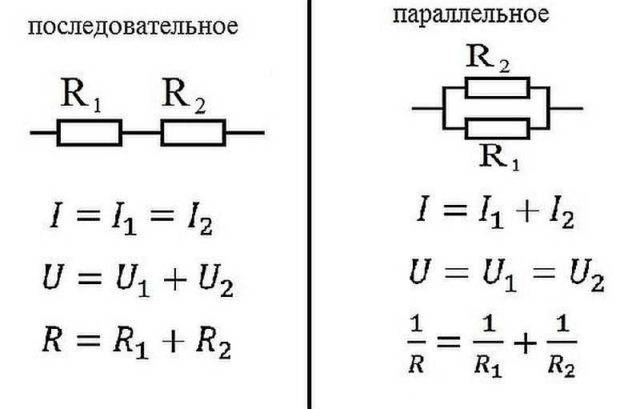
Ohmin laki rinnakkais- ja sarjakytkennälle
sarjaliitäntä
Miten Ohmin laki toimii näissä tapauksissa? Sarjaan kytkettynä elementtiketjun läpi kulkeva virta on sama. Sarjaan kytkettyjen elementtien sisältävän piirin osan jännite lasketaan kunkin osan jännitteiden summana. Miten tämä voidaan selittää? Virran virtaus elementin läpi on osan varauksesta siirtymistä sen osasta toiseen. Tarkoitan, se on työtä. Tämän työn suuruus on jännitystä. Tämä on stressin fyysinen merkitys. Jos tämä on selvää, siirrytään eteenpäin.
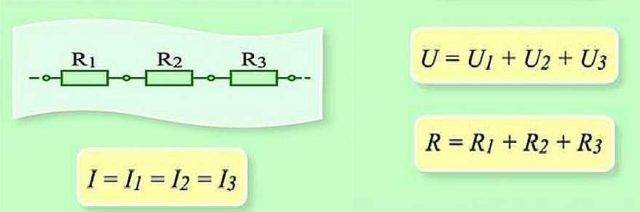
Sarjaliitäntä ja piirin tämän osan parametrit
Sarjaan kytkettynä varaus on siirrettävä vuorotellen jokaisen elementin läpi. Ja jokaisessa elementissä tämä on tietty "työmäärä". Ja löytääksesi työn määrän koko ketjun osalle, sinun on lisättävä työ jokaiseen elementtiin. Joten käy ilmi, että kokonaisjännite on kunkin elementin jännitteiden summa.
Samalla tavalla - summauksen avulla - löydetään myös piiriosan kokonaisresistanssi. Kuinka voit kuvitella sen? Elementtiketjun läpi kulkeva virta voittaa peräkkäin kaikki vastukset. Yksi kerrallaan. Toisin sanoen löytääkseen vastustuksen, jonka hän voitti, on tarpeen laskea yhteen vastukset. Enemmän tai vähemmän näin. Matemaattinen johtaminen on monimutkaisempaa, ja tämän lain mekanismi on helpompi ymmärtää.
Rinnakkaisliitäntä
Rinnakkaiskytkentä on, kun johtimien/elementtien alkukohdat yhtyvät yhdessä pisteessä ja toisessa niiden päät ovat yhteydessä toisiinsa. Yritämme selittää lakeja, jotka ovat voimassa tämän tyyppisille yhdisteille. Aloitetaan nykyisestä. Elementtien liitäntäpisteeseen syötetään jonkin suuruinen virta. Se erottuu ja virtaa kaikkien johtimien läpi. Tästä päättelemme, että osan kokonaisvirta on yhtä suuri kuin kunkin elementin virran summa: I = I1 + I2 + I3.
Nyt jännitteeseen. Jos jännite on työtä varauksen siirtämiseksi, niin työ, joka tarvitaan yhden varauksen siirtämiseen, on sama missä tahansa elementissä. Eli jokaisen rinnakkain kytketyn elementin jännite on sama. U=U1=U2=U3. Ei niin hauskaa ja visuaalista kuin Ohmin lain selitys ketjun osalle, mutta voit ymmärtää.
Rinnakkaisyhteyden lait
Vastustuksen kannalta asiat ovat hieman monimutkaisempia. Otetaan käyttöön johtavuuden käsite. Tämä on ominaisuus, joka osoittaa, kuinka helppoa tai vaikeaa varauksen on kulkea tämän johtimen läpi. On selvää, että mitä pienempi vastus, sitä helpompi virta kulkee. Siksi johtavuus - G - lasketaan vastuksen käänteislukuna. Kaavassa se näyttää tältä: G = 1/R.
Miksi puhumme johtavuudesta? Koska elementtien rinnakkaisliitännällä varustetun osan kokonaisjohtavuus on yhtä suuri kuin kunkin osan johtavuuden summa. G = G1 + G2 + G3 - helppo ymmärtää. Se, kuinka helposti virta voittaa tämän rinnakkaisten elementtien solmun, riippuu kunkin elementin johtavuudesta. Joten käy ilmi, että ne on taitettava.
Nyt voimme siirtyä vastustukseen. Koska johtavuus on resistanssin käänteisluku, saadaan seuraava kaava: 1/R = 1/R1 + 1/R2 + 1/R3.
Mikä antaa meille rinnakkais- ja sarjayhteyden?
Teoreettinen tieto on hyvä asia, mutta kuinka soveltaa sitä käytännössä? Minkä tahansa tyyppisiä elementtejä voidaan kytkeä rinnan ja sarjaan. Mutta harkitsimme vain yksinkertaisimpia lineaarisia elementtejä kuvaavia kaavoja. Lineaariset elementit ovat vastuksia, joita kutsutaan myös "vastuksiksi". Joten näin voit käyttää oppimaasi:
Jos suuriarvoista vastusta ei ole saatavilla, mutta pienempiä on useita, saadaan haluttu resistanssi kytkemällä useita vastuksia sarjaan. Kuten näet, tämä on hyödyllinen tekniikka.
Paristojen käyttöiän pidentämiseksi ne voidaan kytkeä rinnakkain. Tässä tapauksessa jännite Ohmin lain mukaan pysyy samana (voit varmistaa mittaamalla jännitteen yleismittarilla). Ja kaksoispariston "elinikä" on paljon pidempi kuin kahden elementin, jotka korvaavat toisensa
Huomaa vain: vain teholähteitä, joilla on sama potentiaali, voidaan kytkeä rinnan. Eli kuollutta ja uutta akkua ei voi kytkeä.
Jos yhdistät edelleen, akku, jonka varaus on suurempi, yleensä lataa vähemmän ladattua. Tämän seurauksena niiden kokonaisveloitus putoaa alhaiseen arvoon.
Yleensä nämä ovat näiden yhdisteiden yleisimmät käyttötarkoitukset.
Ihanteellinen EMF-lähde
Sähkömotorinen voima (E) on fysikaalinen suure, joka määrittää ulkoisten voimien vaikutuksen asteen liikkeeseen suljetussa varauksenkuljettajien piirissä. Toisin sanoen, kuinka voimakkaasti virralla on taipumus virrata johtimen läpi, riippuu EMF:stä.
Selittäessään tällaisia käsittämättömiä ilmiöitä kotimaiset koulun opettajat haluavat kääntyä hydraulisten analogioiden menetelmään.Jos johdin on putki ja sähkövirta on sen läpi virtaavan veden määrä, niin EMF on paine, jonka pumppu kehittää nesteen pumppaamiseksi.
Termi sähkömotorinen voima liittyy sellaiseen käsitteeseen kuin jännite. Hän, EMF, mitataan myös voltteina (yksikkö - "V"). Jokaisella virtalähteellä, oli se sitten akku, generaattori tai aurinkopaneeli, on oma sähkömoottorivoimansa. Usein tämä EMF on lähellä lähtöjännitettä (U), mutta aina hieman pienempi kuin se. Tämä johtuu lähteen sisäisestä resistanssista, johon osa jännitteestä väistämättä putoaa.
Tästä syystä ihanteellinen EMF-lähde on pikemminkin abstrakti käsite tai fyysinen malli, jolla ei ole paikkaa todellisessa maailmassa, koska akun Rin sisäinen vastus, vaikkakin hyvin alhainen, eroaa silti absoluuttisesta nollasta.
Ihanteellinen ja todellinen emf:n lähde
Differentiaalimuodossa
Kaava esitetään hyvin usein differentiaalisessa muodossa, koska johdin on yleensä epähomogeeninen ja se on tarpeen jakaa mahdollisimman pieniin osiin. Sen läpi kulkeva virta liittyy suuruuteen ja suuntaan, joten sitä pidetään skalaarisuurena. Aina kun johdon läpi kulkeva tuloksena oleva virta on löydettävä, otetaan kaikkien yksittäisten virtojen algebrallinen summa. Koska tämä sääntö koskee vain skalaarisuureita, virtaa pidetään myös skalaarisuureena. Tiedetään, että osan läpi kulkee virta dI = jdS. Sen jännite on yhtä suuri kuin Edl, sitten johdolla, jolla on vakio poikkileikkaus ja yhtä pitkä, suhde on totta:
 Differentiaalinen muoto
Differentiaalinen muoto
Siksi virran ilmaus vektorimuodossa on: j = E.
Tärkeä! Metallijohtimien tapauksessa johtavuus pienenee lämpötilan noustessa, kun taas puolijohteilla se kasvaa. Omovin laki ei osoita tiukkaa oikeasuhteisuutta
Suuren metallien ja metalliseosten joukon vastus häviää lämpötilassa, joka on lähellä absoluuttista nollaa, ja prosessia kutsutaan suprajohtavuudeksi.